A New Medical Diagnosis Method Based on Z-Numbers

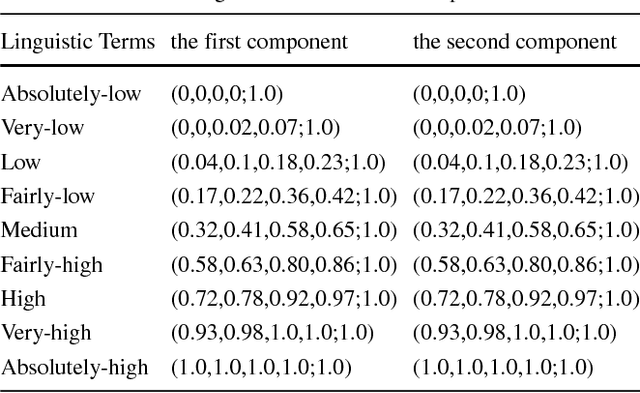
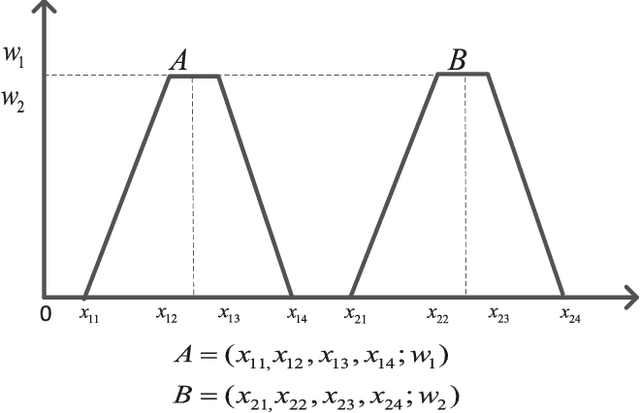
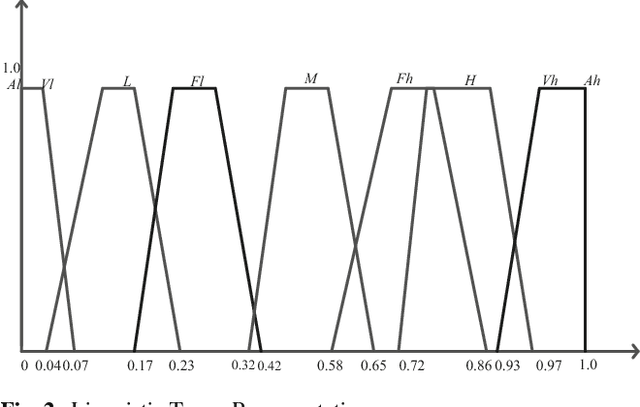
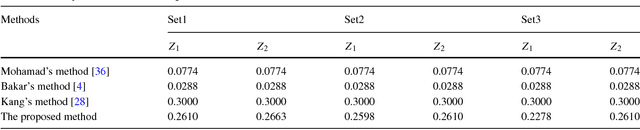
How to handle uncertainty in medical diagnosis is an open issue. In this paper, a new decision making methodology based on Z-numbers is presented. Firstly, the experts' opinions are represented by Z-numbers. Z-number is an ordered pair of fuzzy numbers denoted as Z = (A, B). Then, a new method for ranking fuzzy numbers is proposed. And based on the proposed fuzzy number ranking method, a novel method is presented to transform the Z-numbers into Basic Probability Assignment (BPA). As a result, the information from different sources is combined by the Dempster' combination rule. The final decision making is more reasonable due to the advantage of information fusion. Finally, two experiments, risk analysis and medical diagnosis, are illustrated to show the efficiency of the proposed methodology.

A modified Physarum-inspired model for the user equilibrium traffic assignment problem

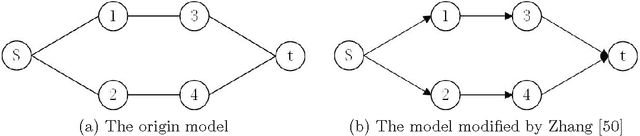
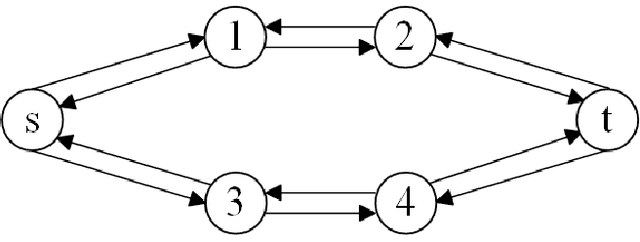
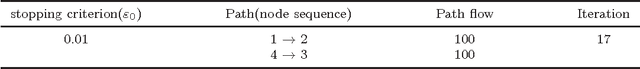
The user equilibrium traffic assignment principle is very important in the traffic assignment problem. Mathematical programming models are designed to solve the user equilibrium problem in traditional algorithms. Recently, the Physarum shows the ability to address the user equilibrium and system optimization traffic assignment problems. However, the Physarum model are not efficient in real traffic networks with two-way traffic characteristics and multiple origin-destination pairs. In this article, a modified Physarum-inspired model for the user equilibrium problem is proposed. By decomposing traffic flux based on origin nodes, the traffic flux from different origin-destination pairs can be distinguished in the proposed model. The Physarum can obtain the equilibrium traffic flux when no shorter path can be discovered between each origin-destination pair. Finally, numerical examples use the Sioux Falls network to demonstrate the rationality and convergence properties of the proposed model.