GCHR : Goal-Conditioned Hindsight Regularization for Sample-Efficient Reinforcement Learning

Goal-conditioned reinforcement learning (GCRL) with sparse rewards remains a fundamental challenge in reinforcement learning. While hindsight experience replay (HER) has shown promise by relabeling collected trajectories with achieved goals, we argue that trajectory relabeling alone does not fully exploit the available experiences in off-policy GCRL methods, resulting in limited sample efficiency. In this paper, we propose Hindsight Goal-conditioned Regularization (HGR), a technique that generates action regularization priors based on hindsight goals. When combined with hindsight self-imitation regularization (HSR), our approach enables off-policy RL algorithms to maximize experience utilization. Compared to existing GCRL methods that employ HER and self-imitation techniques, our hindsight regularizations achieve substantially more efficient sample reuse and the best performances, which we empirically demonstrate on a suite of navigation and manipulation tasks.

MGDA: Model-based Goal Data Augmentation for Offline Goal-conditioned Weighted Supervised Learning

Recently, a state-of-the-art family of algorithms, known as Goal-Conditioned Weighted Supervised Learning (GCWSL) methods, has been introduced to tackle challenges in offline goal-conditioned reinforcement learning (RL). GCWSL optimizes a lower bound of the goal-conditioned RL objective and has demonstrated outstanding performance across diverse goal-reaching tasks, providing a simple, effective, and stable solution. However, prior research has identified a critical limitation of GCWSL: the lack of trajectory stitching capabilities. To address this, goal data augmentation strategies have been proposed to enhance these methods. Nevertheless, existing techniques often struggle to sample suitable augmented goals for GCWSL effectively. In this paper, we establish unified principles for goal data augmentation, focusing on goal diversity, action optimality, and goal reachability. Based on these principles, we propose a Model-based Goal Data Augmentation (MGDA) approach, which leverages a learned dynamics model to sample more suitable augmented goals. MGDA uniquely incorporates the local Lipschitz continuity assumption within the learned model to mitigate the impact of compounding errors. Empirical results show that MGDA significantly enhances the performance of GCWSL methods on both state-based and vision-based maze datasets, surpassing previous goal data augmentation techniques in improving stitching capabilities.

Q-WSL:Leveraging Dynamic Programming for Weighted Supervised Learning in Goal-conditioned RL

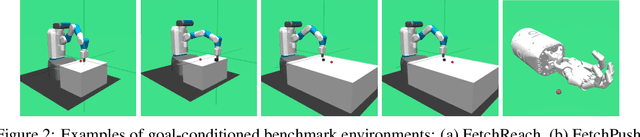
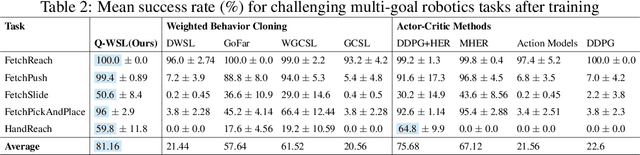
A novel class of advanced algorithms, termed Goal-Conditioned Weighted Supervised Learning (GCWSL), has recently emerged to tackle the challenges posed by sparse rewards in goal-conditioned reinforcement learning (RL). GCWSL consistently delivers strong performance across a diverse set of goal-reaching tasks due to its simplicity, effectiveness, and stability. However, GCWSL methods lack a crucial capability known as trajectory stitching, which is essential for learning optimal policies when faced with unseen skills during testing. This limitation becomes particularly pronounced when the replay buffer is predominantly filled with sub-optimal trajectories. In contrast, traditional TD-based RL methods, such as Q-learning, which utilize Dynamic Programming, do not face this issue but often experience instability due to the inherent difficulties in value function approximation. In this paper, we propose Q-learning Weighted Supervised Learning (Q-WSL), a novel framework designed to overcome the limitations of GCWSL by incorporating the strengths of Dynamic Programming found in Q-learning. Q-WSL leverages Dynamic Programming results to output the optimal action of (state, goal) pairs across different trajectories within the replay buffer. This approach synergizes the strengths of both Q-learning and GCWSL, effectively mitigating their respective weaknesses and enhancing overall performance. Empirical evaluations on challenging goal-reaching tasks demonstrate that Q-WSL surpasses other goal-conditioned approaches in terms of both performance and sample efficiency. Additionally, Q-WSL exhibits notable robustness in environments characterized by binary reward structures and environmental stochasticity.