Distributed Linear Regression with Compositional Covariates

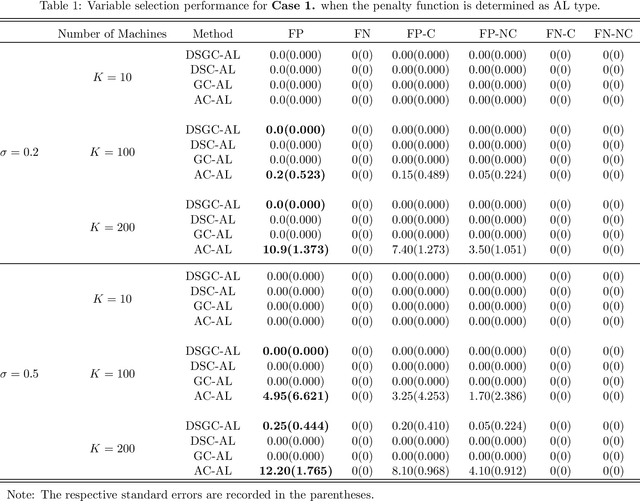
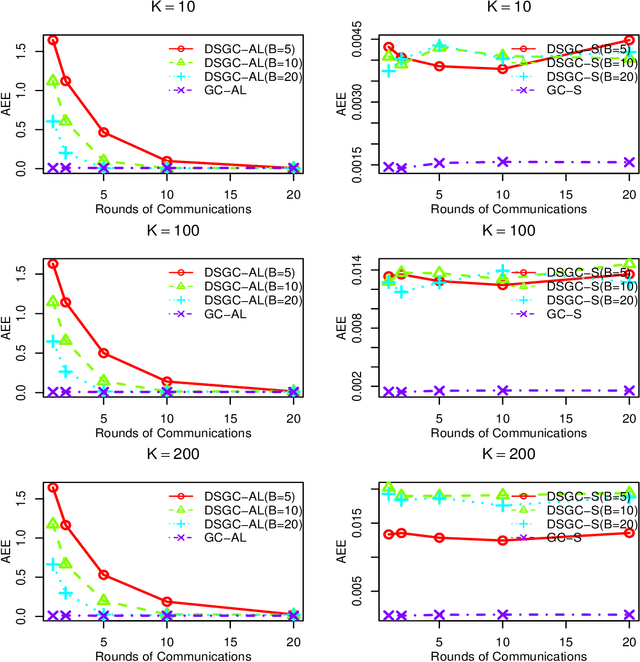
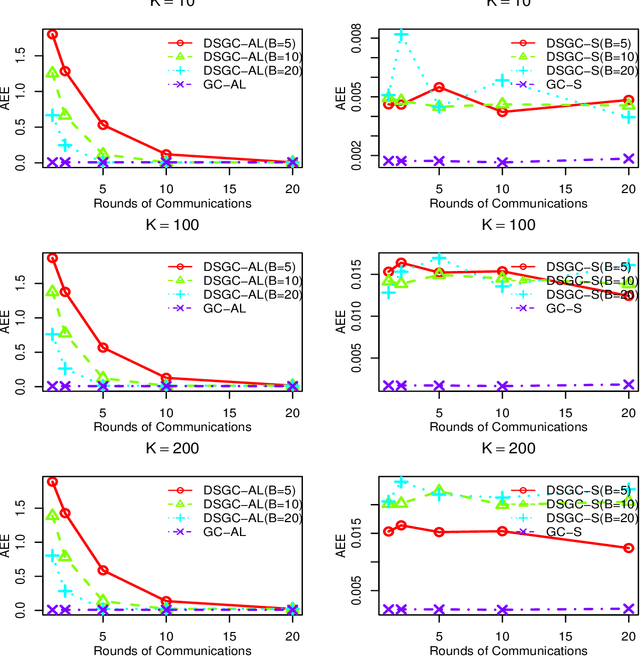
With the availability of extraordinarily huge data sets, solving the problems of distributed statistical methodology and computing for such data sets has become increasingly crucial in the big data area. In this paper, we focus on the distributed sparse penalized linear log-contrast model in massive compositional data. In particular, two distributed optimization techniques under centralized and decentralized topologies are proposed for solving the two different constrained convex optimization problems. Both two proposed algorithms are based on the frameworks of Alternating Direction Method of Multipliers (ADMM) and Coordinate Descent Method of Multipliers(CDMM, Lin et al., 2014, Biometrika). It is worth emphasizing that, in the decentralized topology, we introduce a distributed coordinate-wise descent algorithm based on Group ADMM(GADMM, Elgabli et al., 2020, Journal of Machine Learning Research) for obtaining a communication-efficient regularized estimation. Correspondingly, the convergence theories of the proposed algorithms are rigorously established under some regularity conditions. Numerical experiments on both synthetic and real data are conducted to evaluate our proposed algorithms.

Statistical inference in massive datasets by empirical likelihood

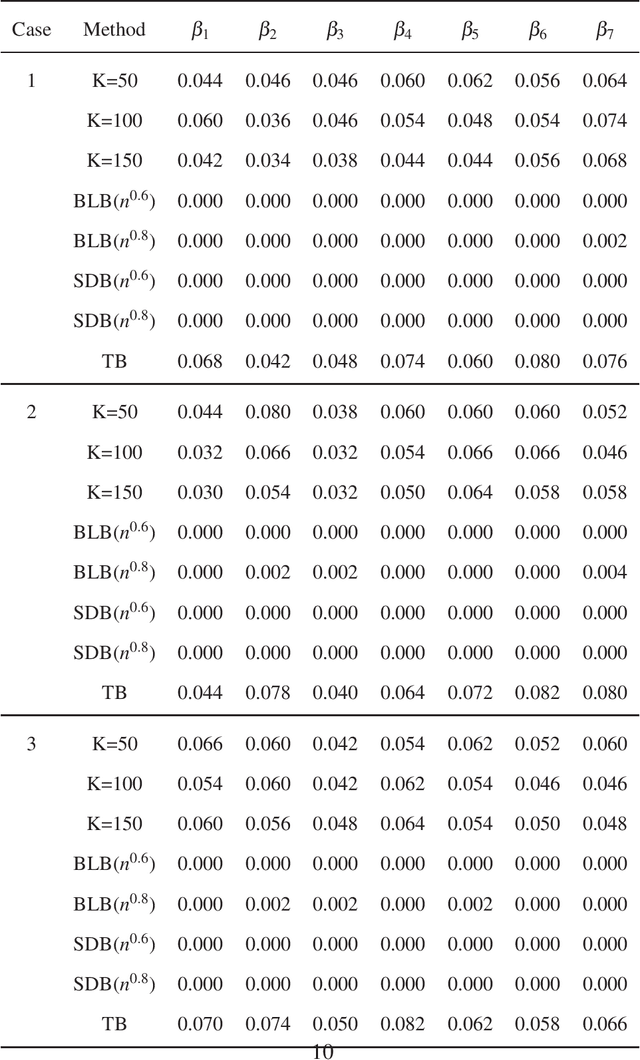
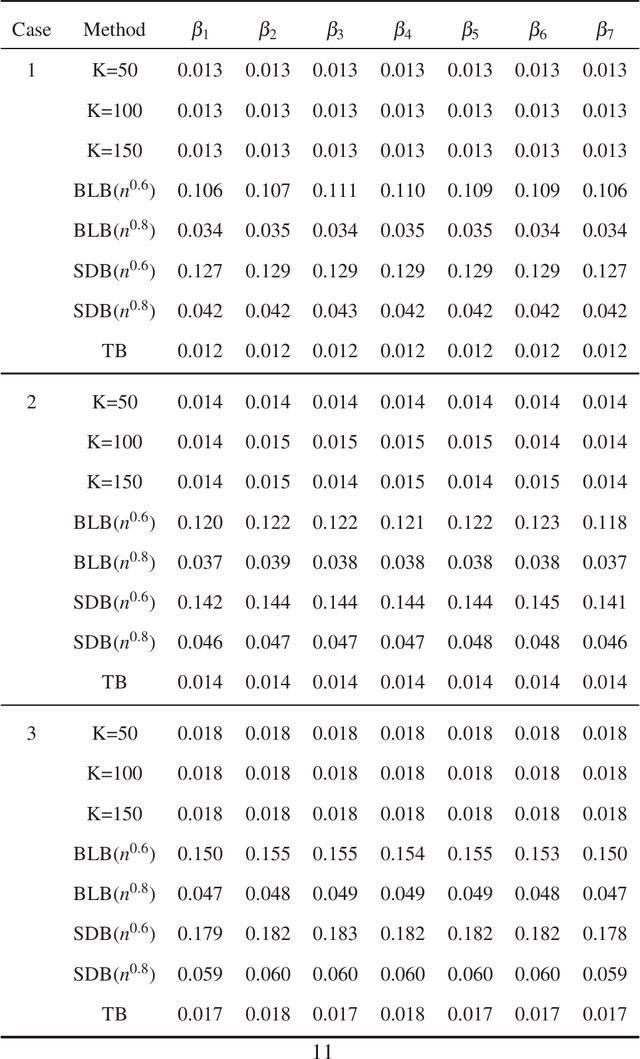
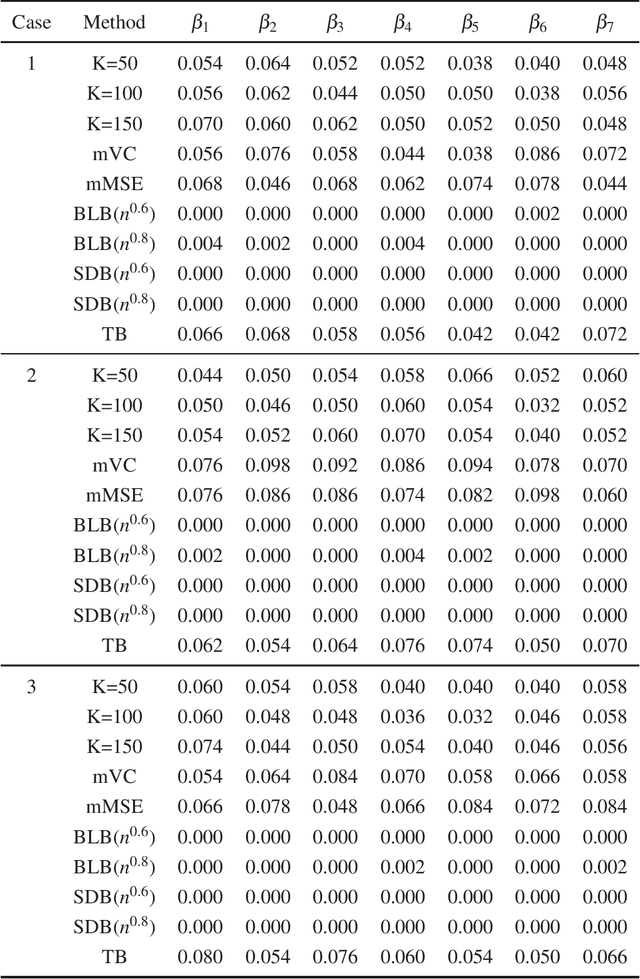
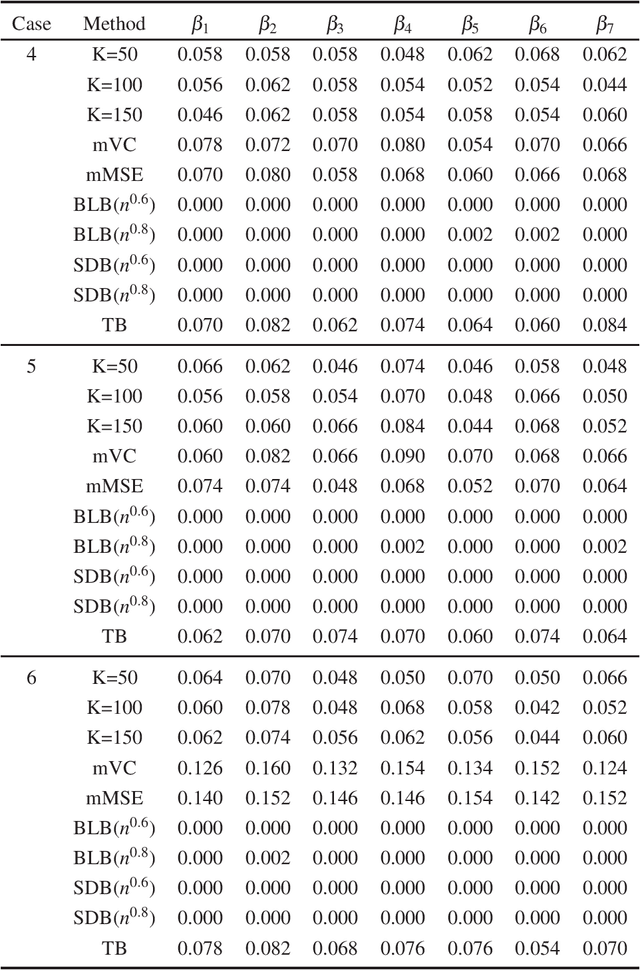
In this paper, we propose a new statistical inference method for massive data sets, which is very simple and efficient by combining divide-and-conquer method and empirical likelihood. Compared with two popular methods (the bag of little bootstrap and the subsampled double bootstrap), we make full use of data sets, and reduce the computation burden. Extensive numerical studies and real data analysis demonstrate the effectiveness and flexibility of our proposed method. Furthermore, the asymptotic property of our method is derived.