Instance-Optimal Matrix Multiplicative Weight Update and Its Quantum Applications

The Matrix Multiplicative Weight Update (MMWU) is a seminal online learning algorithm with numerous applications. Applied to the matrix version of the Learning from Expert Advice (LEA) problem on the $d$-dimensional spectraplex, it is well known that MMWU achieves the minimax-optimal regret bound of $O(\sqrt{T\log d})$, where $T$ is the time horizon. In this paper, we present an improved algorithm achieving the instance-optimal regret bound of $O(\sqrt{T\cdot S(X||d^{-1}I_d)})$, where $X$ is the comparator in the regret, $I_d$ is the identity matrix, and $S(\cdot||\cdot)$ denotes the quantum relative entropy. Furthermore, our algorithm has the same computational complexity as MMWU, indicating that the improvement in the regret bound is ``free''. Technically, we first develop a general potential-based framework for matrix LEA, with MMWU being its special case induced by the standard exponential potential. Then, the crux of our analysis is a new ``one-sided'' Jensen's trace inequality built on a Laplace transform technique, which allows the application of general potential functions beyond exponential to matrix LEA. Our algorithm is finally induced by an optimal potential function from the vector LEA problem, based on the imaginary error function. Complementing the above, we provide a memory lower bound for matrix LEA, and explore the applications of our algorithm in quantum learning theory. We show that it outperforms the state of the art for learning quantum states corrupted by depolarization noise, random quantum states, and Gibbs states. In addition, applying our algorithm to linearized convex losses enables predicting nonlinear quantum properties, such as purity, quantum virtual cooling, and R\'{e}nyi-$2$ correlation.

Adaptive Online Learning of Quantum States

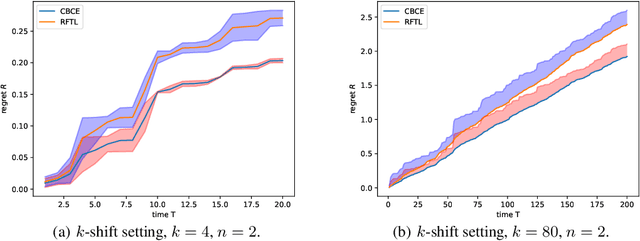
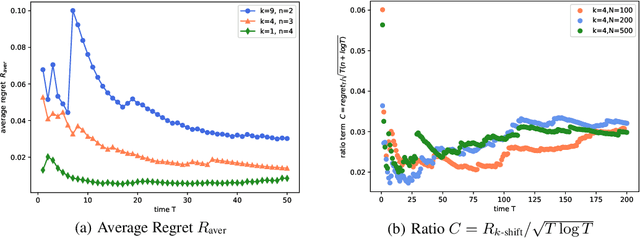
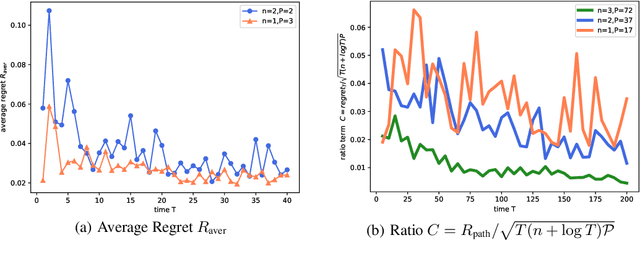
In the fundamental problem of shadow tomography, the goal is to efficiently learn an unknown $d$-dimensional quantum state using projective measurements. However, it is rarely the case that the underlying state remains stationary: changes may occur due to measurements, environmental noise, or an underlying Hamiltonian state evolution. In this paper we adopt tools from adaptive online learning to learn a changing state, giving adaptive and dynamic regret bounds for online shadow tomography that are polynomial in the number of qubits and sublinear in the number of measurements. Our analysis utilizes tools from complex matrix analysis to cope with complex numbers, which may be of independent interest in online learning. In addition, we provide numerical experiments that corroborate our theoretical results.