Adaptive Online Learning of Quantum States
Paper and Code
Jun 01, 2022
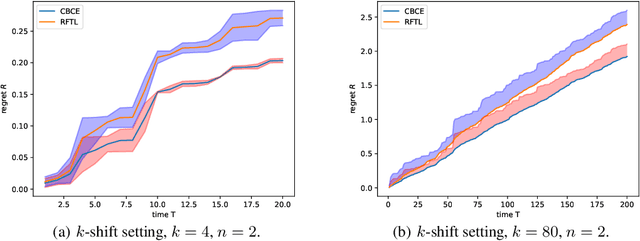
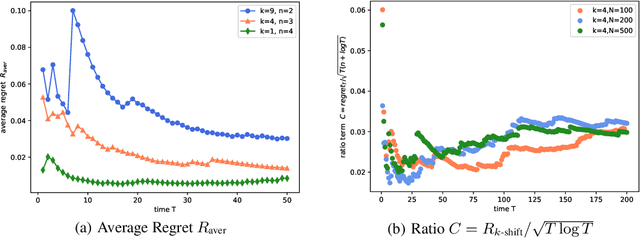
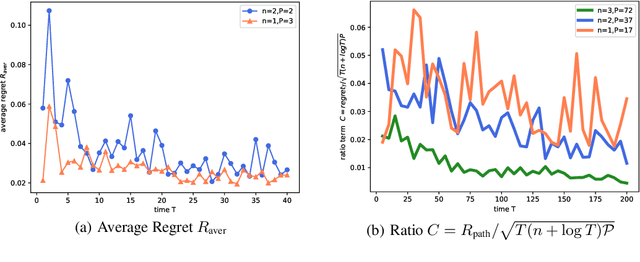
In the fundamental problem of shadow tomography, the goal is to efficiently learn an unknown $d$-dimensional quantum state using projective measurements. However, it is rarely the case that the underlying state remains stationary: changes may occur due to measurements, environmental noise, or an underlying Hamiltonian state evolution. In this paper we adopt tools from adaptive online learning to learn a changing state, giving adaptive and dynamic regret bounds for online shadow tomography that are polynomial in the number of qubits and sublinear in the number of measurements. Our analysis utilizes tools from complex matrix analysis to cope with complex numbers, which may be of independent interest in online learning. In addition, we provide numerical experiments that corroborate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge