Optimal and Bounded-Suboptimal Multi-Goal Task Assignment and Path Finding

We formalize and study the multi-goal task assignment and path finding (MG-TAPF) problem from theoretical and algorithmic perspectives. The MG-TAPF problem is to compute an assignment of tasks to agents, where each task consists of a sequence of goal locations, and collision-free paths for the agents that visit all goal locations of their assigned tasks in sequence. Theoretically, we prove that the MG-TAPF problem is NP-hard to solve optimally. We present algorithms that build upon algorithmic techniques for the multi-agent path finding problem and solve the MG-TAPF problem optimally and bounded-suboptimally. We experimentally compare these algorithms on a variety of different benchmark domains.

Emergent organization of receptive fields in networks of excitatory and inhibitory neurons

Local patterns of excitation and inhibition that can generate neural waves are studied as a computational mechanism underlying the organization of neuronal tunings. Sparse coding algorithms based on networks of excitatory and inhibitory neurons are proposed that exhibit topographic maps as the receptive fields are adapted to input stimuli. Motivated by a leaky integrate-and-fire model of neural waves, we propose an activation model that is more typical of artificial neural networks. Computational experiments with the activation model using both natural images and natural language text are presented. In the case of images, familiar "pinwheel" patterns of oriented edge detectors emerge; in the case of text, the resulting topographic maps exhibit a 2-dimensional representation of granular word semantics. Experiments with a synthetic model of somatosensory input are used to investigate how the network dynamics may affect plasticity of neuronal maps under changes to the inputs.

Empirical Bayes PCA in high dimensions

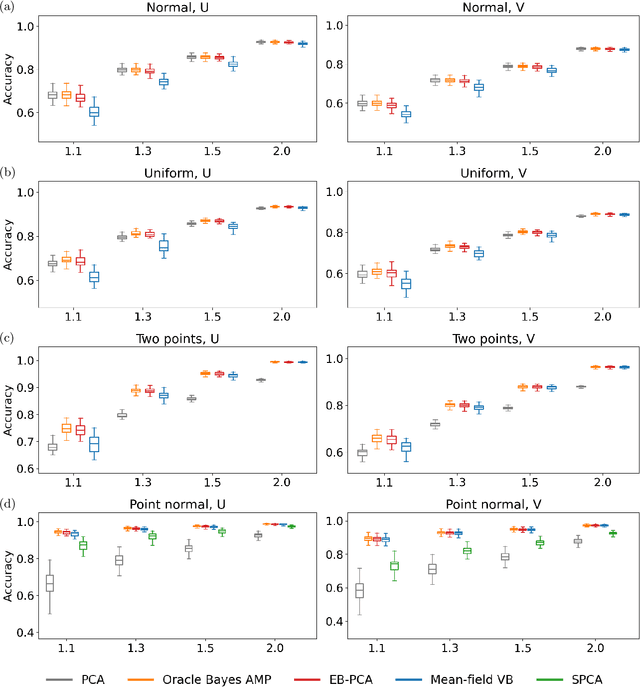
When the dimension of data is comparable to or larger than the number of available data samples, Principal Components Analysis (PCA) is known to exhibit problematic phenomena of high-dimensional noise. In this work, we propose an Empirical Bayes PCA method that reduces this noise by estimating a structural prior for the joint distributions of the principal components. This EB-PCA method is based upon the classical Kiefer-Wolfowitz nonparametric MLE for empirical Bayes estimation, distributional results derived from random matrix theory for the sample PCs, and iterative refinement using an Approximate Message Passing (AMP) algorithm. In theoretical "spiked" models, EB-PCA achieves Bayes-optimal estimation accuracy in the same settings as the oracle Bayes AMP procedure that knows the true priors. Empirically, EB-PCA can substantially improve over PCA when there is strong prior structure, both in simulation and on several quantitative benchmarks constructed using data from the 1000 Genomes Project and the International HapMap Project. A final illustration is presented for an analysis of gene expression data obtained by single-cell RNA-seq.