Empirical Bayes PCA in high dimensions

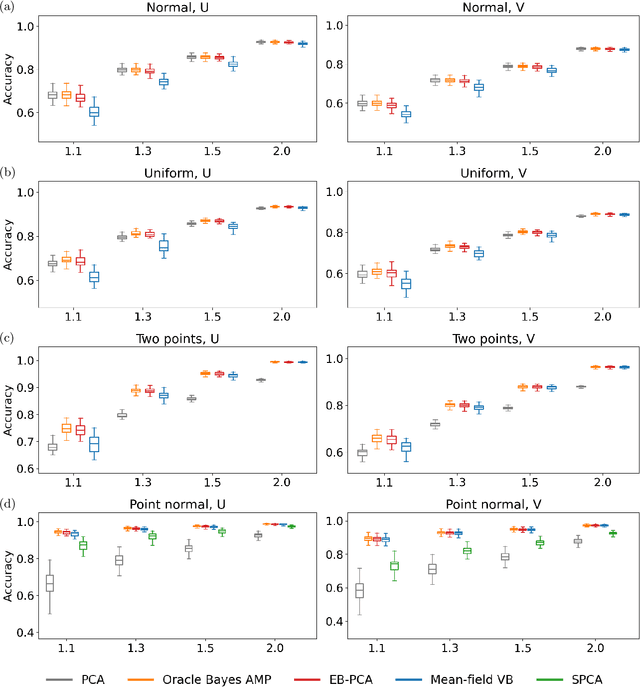
When the dimension of data is comparable to or larger than the number of available data samples, Principal Components Analysis (PCA) is known to exhibit problematic phenomena of high-dimensional noise. In this work, we propose an Empirical Bayes PCA method that reduces this noise by estimating a structural prior for the joint distributions of the principal components. This EB-PCA method is based upon the classical Kiefer-Wolfowitz nonparametric MLE for empirical Bayes estimation, distributional results derived from random matrix theory for the sample PCs, and iterative refinement using an Approximate Message Passing (AMP) algorithm. In theoretical "spiked" models, EB-PCA achieves Bayes-optimal estimation accuracy in the same settings as the oracle Bayes AMP procedure that knows the true priors. Empirically, EB-PCA can substantially improve over PCA when there is strong prior structure, both in simulation and on several quantitative benchmarks constructed using data from the 1000 Genomes Project and the International HapMap Project. A final illustration is presented for an analysis of gene expression data obtained by single-cell RNA-seq.