DF2M: An Explainable Deep Bayesian Nonparametric Model for High-Dimensional Functional Time Series

In this paper, we present Deep Functional Factor Model (DF2M), a Bayesian nonparametric model for analyzing high-dimensional functional time series. The DF2M makes use of the Indian Buffet Process and the multi-task Gaussian Process with a deep kernel function to capture non-Markovian and nonlinear temporal dynamics. Unlike many black-box deep learning models, the DF2M provides an explainable way to use neural networks by constructing a factor model and incorporating deep neural networks within the kernel function. Additionally, we develop a computationally efficient variational inference algorithm for inferring the DF2M. Empirical results from four real-world datasets demonstrate that the DF2M offers better explainability and superior predictive accuracy compared to conventional deep learning models for high-dimensional functional time series.

EEGNN: Edge Enhanced Graph Neural Networks

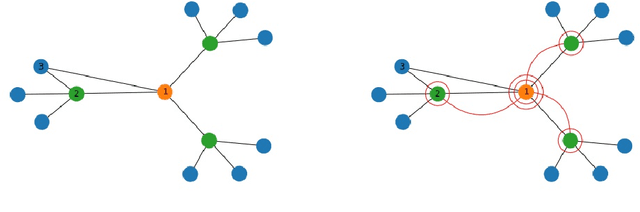
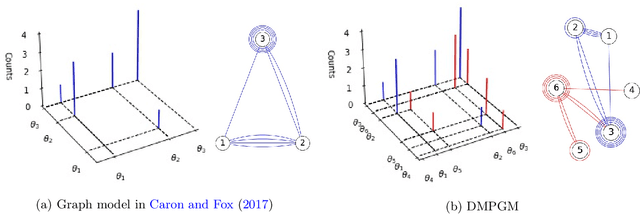
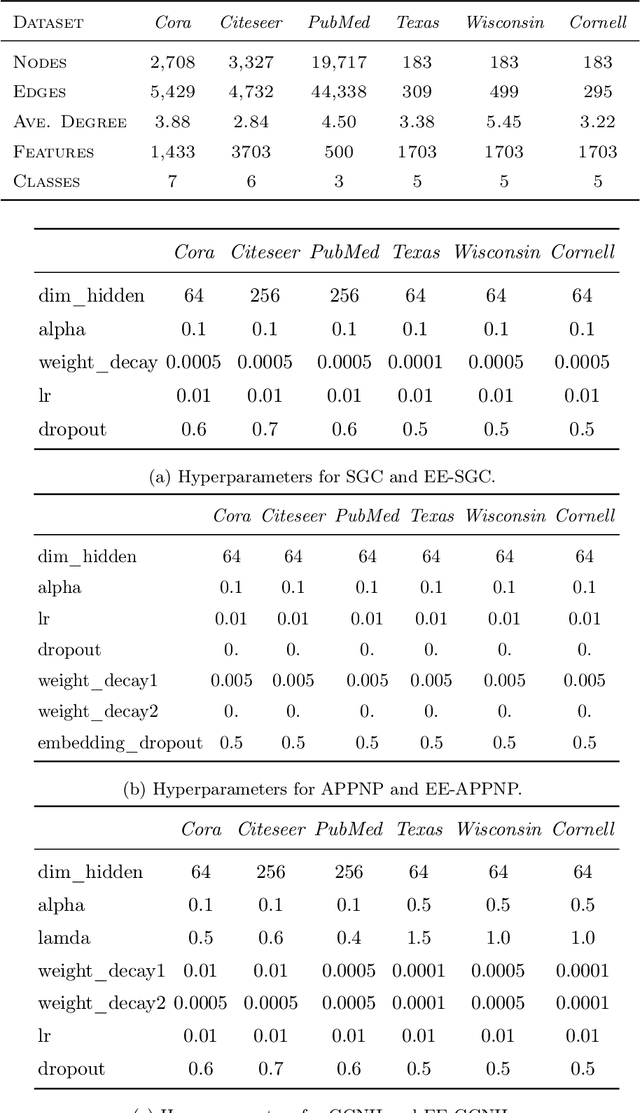
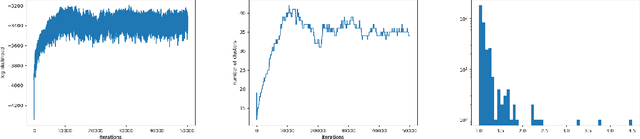
Training deep graph neural networks (GNNs) poses a challenging task, as the performance of GNNs may suffer from the number of hidden message-passing layers. The literature has focused on the proposals of over-smoothing and under-reaching to explain the performance deterioration of deep GNNs. In this paper, we propose a new explanation for such deteriorated performance phenomenon, mis-simplification, that is, mistakenly simplifying graphs by preventing self-loops and forcing edges to be unweighted. We show that such simplifying can reduce the potential of message-passing layers to capture the structural information of graphs. In view of this, we propose a new framework, edge enhanced graph neural network(EEGNN). EEGNN uses the structural information extracted from the proposed Dirichlet mixture Poisson graph model, a Bayesian nonparametric model for graphs, to improve the performance of various deep message-passing GNNs. Experiments over different datasets show that our method achieves considerable performance increase compared to baselines.

Conditional Variational Inference with Adaptive Truncation for Bayesian Nonparametric Models

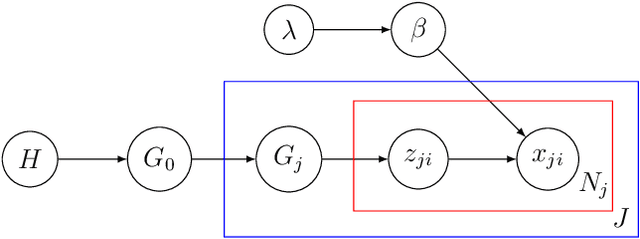
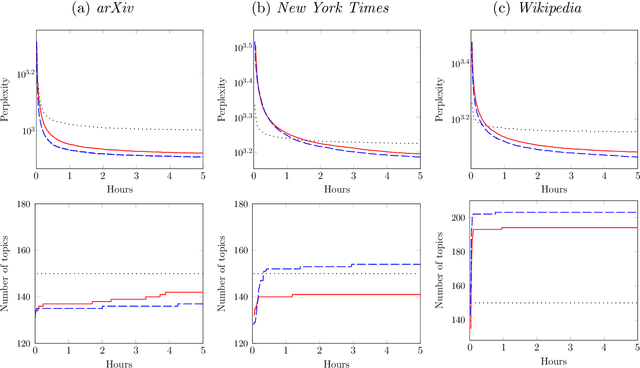
The scalable inference for Bayesian nonparametric models with big data is still challenging. Current variational inference methods fail to characterise the correlation structure among latent variables due to the mean-field setting and cannot infer the true posterior dimension because of the universal truncation. To overcome these limitations, we build a general framework to infer Bayesian nonparametric models by maximising the proposed nonparametric evidence lower bound, and then develop a novel approach by combining Monte Carlo sampling and stochastic variational inference framework. Our method has several advantages over the traditional online variational inference method. First, it achieves a smaller divergence between variational distributions and the true posterior by factorising variational distributions under the conditional setting instead of the mean-field setting to capture the correlation pattern. Second, it reduces the risk of underfitting or overfitting by truncating the dimension adaptively rather than using a prespecified truncated dimension for all latent variables. Third, it reduces the computational complexity by approximating the posterior functionally instead of updating the stick-breaking parameters individually. We apply the proposed method on hierarchical Dirichlet process and gamma--Dirichlet process models, two essential Bayesian nonparametric models in topic analysis. The empirical study on three large datasets including arXiv, New York Times and Wikipedia reveals that our proposed method substantially outperforms its competitor in terms of lower perplexity and much clearer topic-words clustering.