Xingao Gong
An Agentic Framework for Autonomous Materials Computation
Dec 22, 2025



Abstract:Large Language Models (LLMs) have emerged as powerful tools for accelerating scientific discovery, yet their static knowledge and hallucination issues hinder autonomous research applications. Recent advances integrate LLMs into agentic frameworks, enabling retrieval, reasoning, and tool use for complex scientific workflows. Here, we present a domain-specialized agent designed for reliable automation of first-principles materials computations. By embedding domain expertise, the agent ensures physically coherent multi-step workflows and consistently selects convergent, well-posed parameters, thereby enabling reliable end-to-end computational execution. A new benchmark of diverse computational tasks demonstrates that our system significantly outperforms standalone LLMs in both accuracy and robustness. This work establishes a verifiable foundation for autonomous computational experimentation and represents a key step toward fully automated scientific discovery.
Universal Machine Learning Kohn-Sham Hamiltonian for Materials
Feb 14, 2024Abstract:While density functional theory (DFT) serves as a prevalent computational approach in electronic structure calculations, its computational demands and scalability limitations persist. Recently, leveraging neural networks to parameterize the Kohn-Sham DFT Hamiltonian has emerged as a promising avenue for accelerating electronic structure computations. Despite advancements, challenges such as the necessity for computing extensive DFT training data to explore new systems and the complexity of establishing accurate ML models for multi-elemental materials still exist. Addressing these hurdles, this study introduces a universal electronic Hamiltonian model trained on Hamiltonian matrices obtained from first-principles DFT calculations of nearly all crystal structures on the Materials Project. We demonstrate its generality in predicting electronic structures across the whole periodic table, including complex multi-elemental systems. By offering a reliable efficient framework for computing electronic properties, this universal Hamiltonian model lays the groundwork for advancements in diverse fields related to electronic structures.
Capturing long-range interaction with reciprocal space neural network
Nov 30, 2022Abstract:Machine Learning (ML) interatomic models and potentials have been widely employed in simulations of materials. Long-range interactions often dominate in some ionic systems whose dynamics behavior is significantly influenced. However, the long-range effect such as Coulomb and Van der Wales potential is not considered in most ML interatomic potentials. To address this issue, we put forward a method that can take long-range effects into account for most ML local interatomic models with the reciprocal space neural network. The structure information in real space is firstly transformed into reciprocal space and then encoded into a reciprocal space potential or a global descriptor with full atomic interactions. The reciprocal space potential and descriptor keep full invariance of Euclidean symmetry and choice of the cell. Benefiting from the reciprocal-space information, ML interatomic models can be extended to describe the long-range potential including not only Coulomb but any other long-range interaction. A model NaCl system considering Coulomb interaction and the GaxNy system with defects are applied to illustrate the advantage of our approach. At the same time, our approach helps to improve the prediction accuracy of some global properties such as the band gap where the full atomic interaction beyond local atomic environments plays a very important role. In summary, our work has expanded the ability of current ML interatomic models and potentials when dealing with the long-range effect, hence paving a new way for accurate prediction of global properties and large-scale dynamic simulations of systems with defects.
Time-reversal equivariant neural network potential and Hamiltonian for magnetic materials
Nov 21, 2022Abstract:This work presents Time-reversal Equivariant Neural Network (TENN) framework. With TENN, the time-reversal symmetry is considered in the equivariant neural network (ENN), which generalizes the ENN to consider physical quantities related to time-reversal symmetry such as spin and velocity of atoms. TENN-e3, as the time-reversal-extension of E(3) equivariant neural network, is developed to keep the Time-reversal E(3) equivariant with consideration of whether to include the spin-orbit effect for both collinear and non-collinear magnetic moments situations for magnetic material. TENN-e3 can construct spin neural network potential and the Hamiltonian of magnetic material from ab-initio calculations. Time-reversal-E(3)-equivariant convolutions for interactions of spinor and geometric tensors are employed in TENN-e3. Compared to the popular ENN, TENN-e3 can describe the complex spin-lattice coupling with high accuracy and keep time-reversal symmetry which is not preserved in the existing E(3)-equivariant model. Also, the Hamiltonian of magnetic material with time-reversal symmetry can be built with TENN-e3. TENN paves a new way to spin-lattice dynamics simulations over long-time scales and electronic structure calculations of large-scale magnetic materials.
Transferable E(3) equivariant parameterization for Hamiltonian of molecules and solids
Oct 28, 2022Abstract:Machine learning, especially deep learning, can build a direct mapping from structure to properties with its huge parameter space, making it possible to perform high-throughput screening for the desired properties of materials. However, since the electronic Hamiltonian transforms non-trivially under rotation operations, it is challenging to accurately predict the electronic Hamiltonian while strictly satisfying this constraint. There is currently a lack of transferable machine learning models that can bypass the computationally demanding density functional theory (DFT) to obtain the ab initio Hamiltonian of molecules and materials by complete data-driven methods. In this work, we point out the necessity of explicitly considering the parity symmetry of the electronic Hamiltonian in addition to rotational equivariance. We propose a parameterized Hamiltonian that strictly satisfies rotational equivariance and parity symmetry simultaneously, based on which we develop an E(3) equivariant neural network called HamNet to predict the ab initio tight-binding Hamiltonian of various molecules and solids. The tests show that this model has similar transferability to that of machine learning potentials and can be applied to a class of materials with different configurations using the same set of trained network weights. The proposed framework provides a general transferable model for accelerating electronic structure calculations.
Graph Neural Network Potential for Magnetic Materials
Mar 06, 2022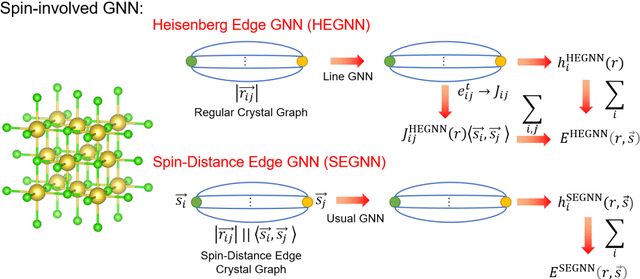
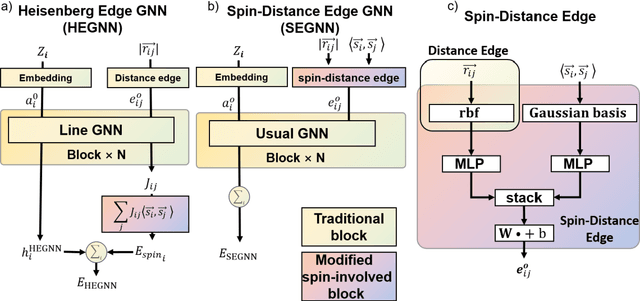
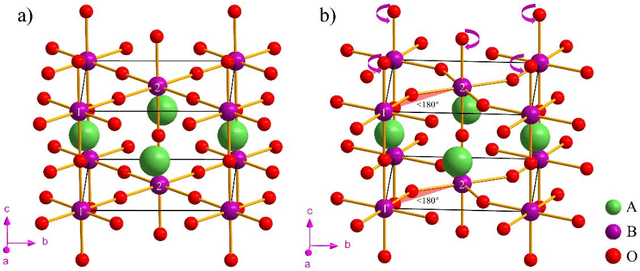
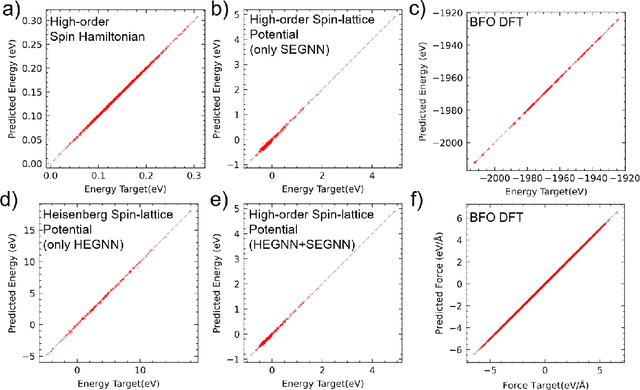
Abstract:Machine Learning (ML) interatomic potential has shown its great power in condensed matter physics. However, ML interatomic potential for a magnetic system including both structural degrees of freedom and magnetic moments has not been well developed yet. A spin-dependent ML interatomic potential approach based on the crystal graph neural network (GNN) has been developed for any magnetic system. It consists of the Heisenberg edge graph neural network (HEGNN) and spin-distance edge graph neural network (SEGNN). The network captures the Heisenberg coefficient variation between different structures and the fine spin-lattice coupling of high order and multi-body interaction with high accuracy. In the tests, this method perfectly fitted a high-order spin Hamiltonian and two complex spin-lattice Hamiltonian and captured the fine spin-lattice coupling in BiFeO3. In addition, a disturbed structure of BiFeO3 with strain was successfully optimized with the trained potential. Our work has expanded the powerful ML GNN potentials to magnetic systems, which paves a new way for large-scale dynamic simulations on spin-lattice coupled systems.
Edge-based Tensor prediction via graph neural networks
Jan 15, 2022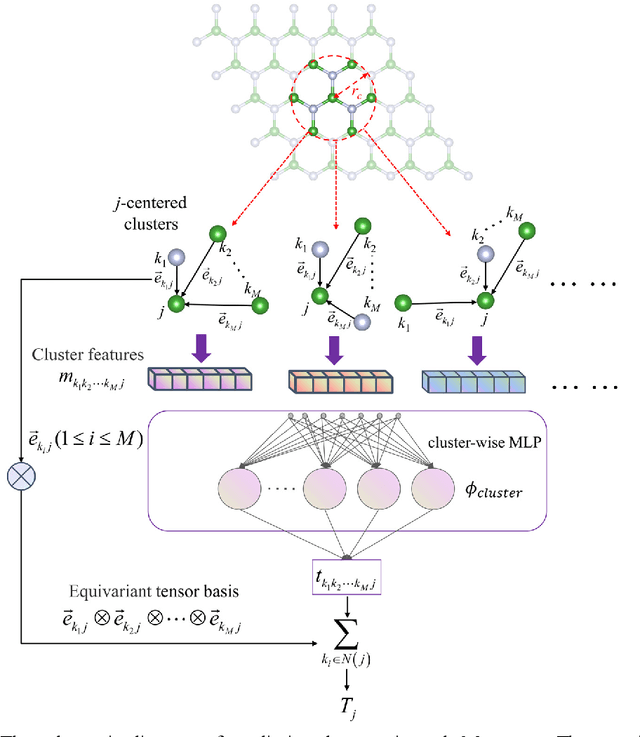
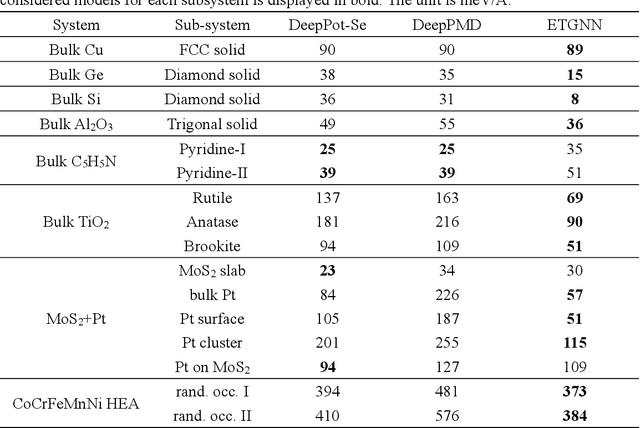
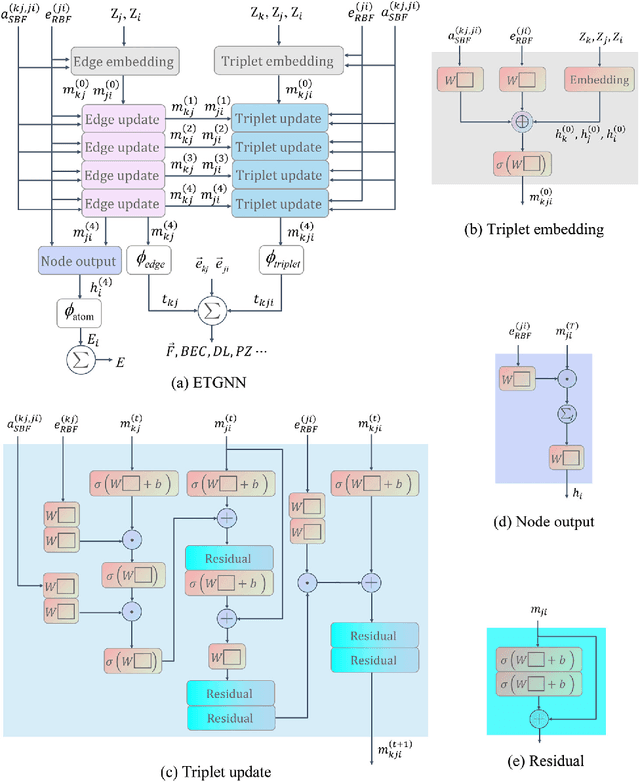
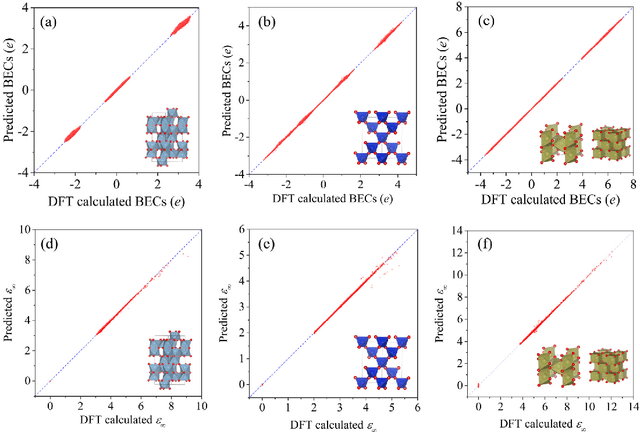
Abstract:Message-passing neural networks (MPNN) have shown extremely high efficiency and accuracy in predicting the physical properties of molecules and crystals, and are expected to become the next-generation material simulation tool after the density functional theory (DFT). However, there is currently a lack of a general MPNN framework for directly predicting the tensor properties of the crystals. In this work, a general framework for the prediction of tensor properties was proposed: the tensor property of a crystal can be decomposed into the average of the tensor contributions of all the atoms in the crystal, and the tensor contribution of each atom can be expanded as the sum of the tensor projections in the directions of the edges connecting the atoms. On this basis, the edge-based expansions of force vectors, Born effective charges (BECs), dielectric (DL) and piezoelectric (PZ) tensors were proposed. These expansions are rotationally equivariant, while the coefficients in these tensor expansions are rotationally invariant scalars which are similar to physical quantities such as formation energy and band gap. The advantage of this tensor prediction framework is that it does not require the network itself to be equivariant. Therefore, in this work, we directly designed the edge-based tensor prediction graph neural network (ETGNN) model on the basis of the invariant graph neural network to predict tensors. The validity and high precision of this tensor prediction framework were shown by the tests of ETGNN on the extended systems, random perturbed structures and JARVIS-DFT datasets. This tensor prediction framework is general for nearly all the GNNs and can achieve higher accuracy with more advanced GNNs in the future.
Complex Spin Hamiltonian Represented by Artificial Neural Network
Oct 02, 2021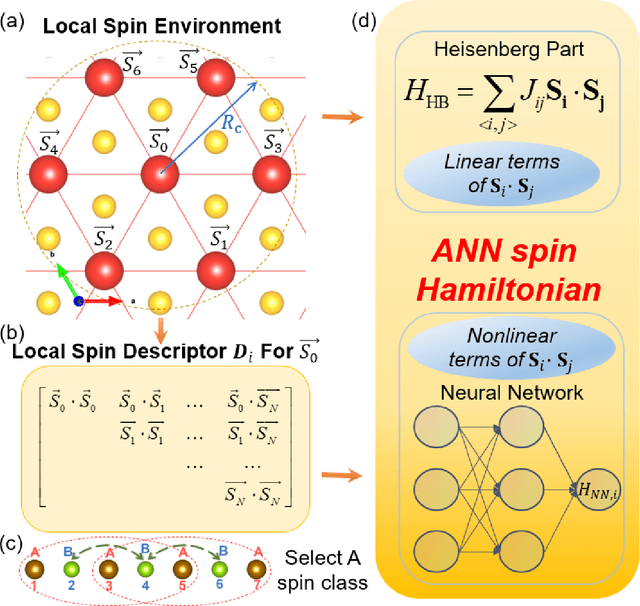
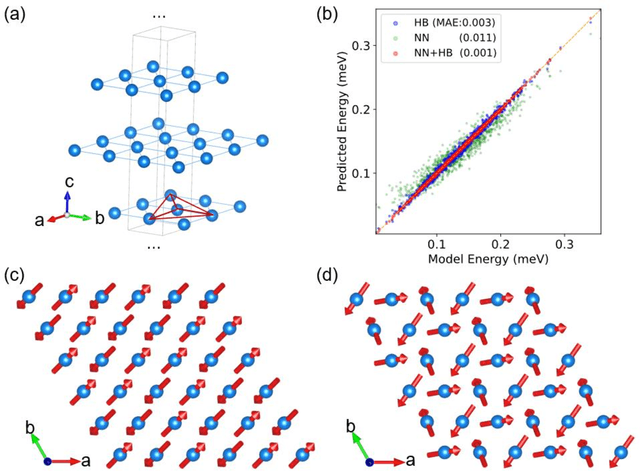
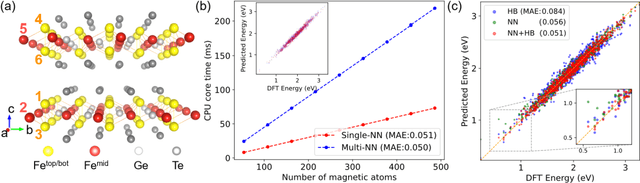
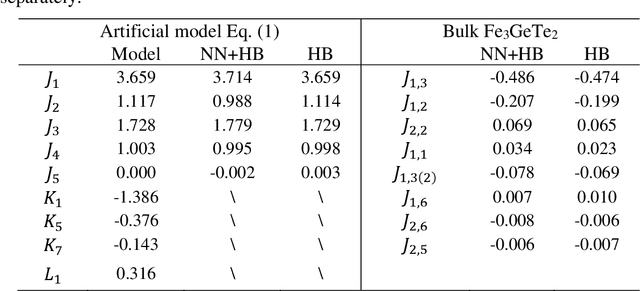
Abstract:The effective spin Hamiltonian method is widely adopted to simulate and understand the behavior of magnetism. However, the magnetic interactions of some systems, such as itinerant magnets, are too complex to be described by any explicit function, which prevents an accurate description of magnetism in such systems. Here, we put forward a machine learning (ML) approach, applying an artificial neural network (ANN) and a local spin descriptor to develop effective spin potentials for any form of interaction. The constructed Hamiltonians include an explicit Heisenberg part and an implicit non-linear ANN part. Such a method successfully reproduces artificially constructed models and also sufficiently describe the itinerant magnetism of bulk Fe3GeTe2. Our work paves a new way for investigating complex magnetic phenomena (e.g., skyrmions) of magnetic materials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge