On-the-fly machine learning for parametrization of the effective Hamiltonian

The first-principles-based effective Hamiltonian is widely used to predict and simulate the properties of ferroelectrics and relaxor ferroelectrics. However, the parametrization method of the effective Hamiltonian is complicated and hardly can resolve the systems with complex interactions and/or complex components. Here, we developed an on-the-fly machine learning approach to parametrize the effective Hamiltonian based on Bayesian linear regression. The parametrization is completed in molecular dynamics simulations, with the energy, forces and stress predicted at each step along with their uncertainties. First-principles calculations are executed when the uncertainties are large to retrain the parameters. This approach provides a universal and automatic way to compute the effective Hamiltonian parameters for any considered systems including complex systems which previous methods can not handle. BaTiO3 and Pb(Sc,Ta)O3 are taken as examples to show the accurateness of this approach comparing with conventional first-principles parametrization method.

Complex Spin Hamiltonian Represented by Artificial Neural Network

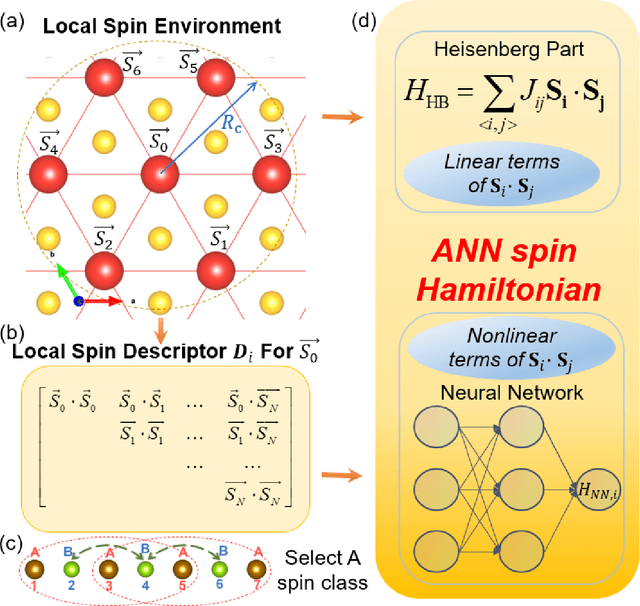
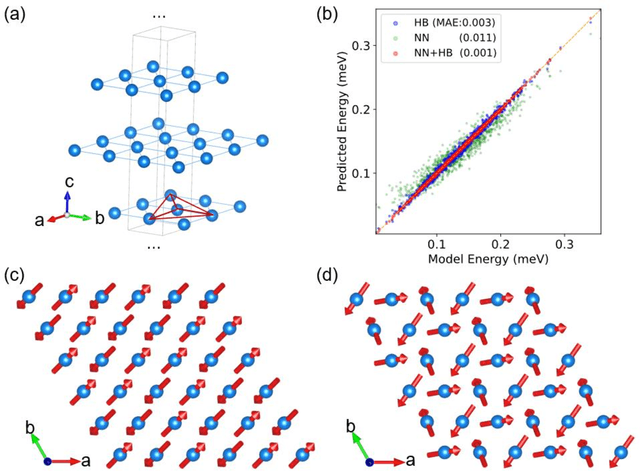
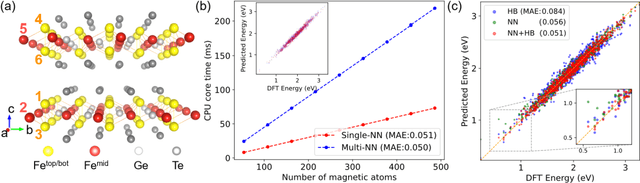
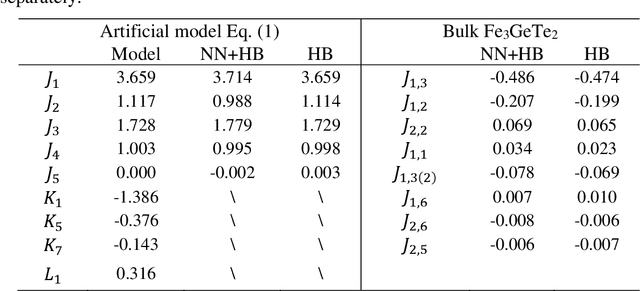
The effective spin Hamiltonian method is widely adopted to simulate and understand the behavior of magnetism. However, the magnetic interactions of some systems, such as itinerant magnets, are too complex to be described by any explicit function, which prevents an accurate description of magnetism in such systems. Here, we put forward a machine learning (ML) approach, applying an artificial neural network (ANN) and a local spin descriptor to develop effective spin potentials for any form of interaction. The constructed Hamiltonians include an explicit Heisenberg part and an implicit non-linear ANN part. Such a method successfully reproduces artificially constructed models and also sufficiently describe the itinerant magnetism of bulk Fe3GeTe2. Our work paves a new way for investigating complex magnetic phenomena (e.g., skyrmions) of magnetic materials.