Representation-Enhanced Neural Knowledge Integration with Application to Large-Scale Medical Ontology Learning

A large-scale knowledge graph enhances reproducibility in biomedical data discovery by providing a standardized, integrated framework that ensures consistent interpretation across diverse datasets. It improves generalizability by connecting data from various sources, enabling broader applicability of findings across different populations and conditions. Generating reliable knowledge graph, leveraging multi-source information from existing literature, however, is challenging especially with a large number of node sizes and heterogeneous relations. In this paper, we propose a general theoretically guaranteed statistical framework, called RENKI, to enable simultaneous learning of multiple relation types. RENKI generalizes various network models widely used in statistics and computer science. The proposed framework incorporates representation learning output into initial entity embedding of a neural network that approximates the score function for the knowledge graph and continuously trains the model to fit observed facts. We prove nonasymptotic bounds for in-sample and out-of-sample weighted MSEs in relation to the pseudo-dimension of the knowledge graph function class. Additionally, we provide pseudo-dimensions for score functions based on multilayer neural networks with ReLU activation function, in the scenarios when the embedding parameters either fixed or trainable. Finally, we complement our theoretical results with numerical studies and apply the method to learn a comprehensive medical knowledge graph combining a pretrained language model representation with knowledge graph links observed in several medical ontologies. The experiments justify our theoretical findings and demonstrate the effect of weighting in the presence of heterogeneous relations and the benefit of incorporating representation learning in nonparametric models.

Globally-Optimal Greedy Experiment Selection for Active Sequential Estimation

Motivated by modern applications such as computerized adaptive testing, sequential rank aggregation, and heterogeneous data source selection, we study the problem of active sequential estimation, which involves adaptively selecting experiments for sequentially collected data. The goal is to design experiment selection rules for more accurate model estimation. Greedy information-based experiment selection methods, optimizing the information gain for one-step ahead, have been employed in practice thanks to their computational convenience, flexibility to context or task changes, and broad applicability. However, statistical analysis is restricted to one-dimensional cases due to the problem's combinatorial nature and the seemingly limited capacity of greedy algorithms, leaving the multidimensional problem open. In this study, we close the gap for multidimensional problems. In particular, we propose adopting a class of greedy experiment selection methods and provide statistical analysis for the maximum likelihood estimator following these selection rules. This class encompasses both existing methods and introduces new methods with improved numerical efficiency. We prove that these methods produce consistent and asymptotically normal estimators. Additionally, within a decision theory framework, we establish that the proposed methods achieve asymptotic optimality when the risk measure aligns with the selection rule. We also conduct extensive numerical studies on both simulated and real data to illustrate the efficacy of the proposed methods. From a technical perspective, we devise new analytical tools to address theoretical challenges. These analytical tools are of independent theoretical interest and may be reused in related problems involving stochastic approximation and sequential designs.

A Generalized Latent Factor Model Approach to Mixed-data Matrix Completion with Entrywise Consistency

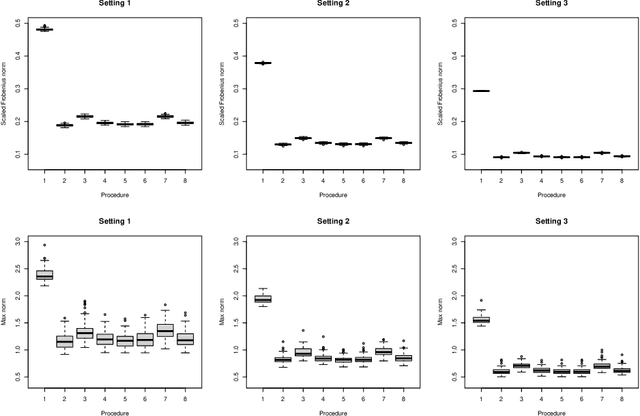
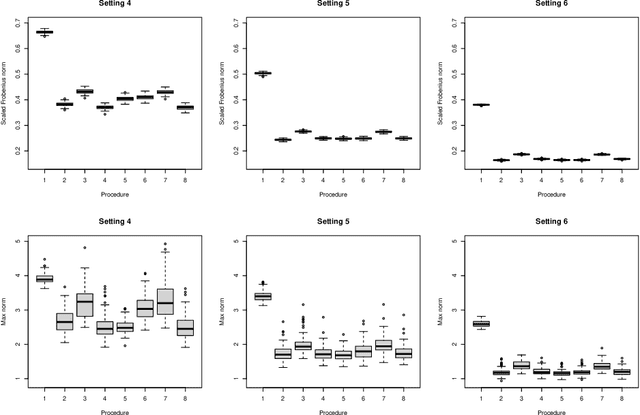
Matrix completion is a class of machine learning methods that concerns the prediction of missing entries in a partially observed matrix. This paper studies matrix completion for mixed data, i.e., data involving mixed types of variables (e.g., continuous, binary, ordinal). We formulate it as a low-rank matrix estimation problem under a general family of non-linear factor models and then propose entrywise consistent estimators for estimating the low-rank matrix. Tight probabilistic error bounds are derived for the proposed estimators. The proposed methods are evaluated by simulation studies and real-data applications for collaborative filtering and large-scale educational assessment.