A Generalized Latent Factor Model Approach to Mixed-data Matrix Completion with Entrywise Consistency
Paper and Code
Nov 17, 2022
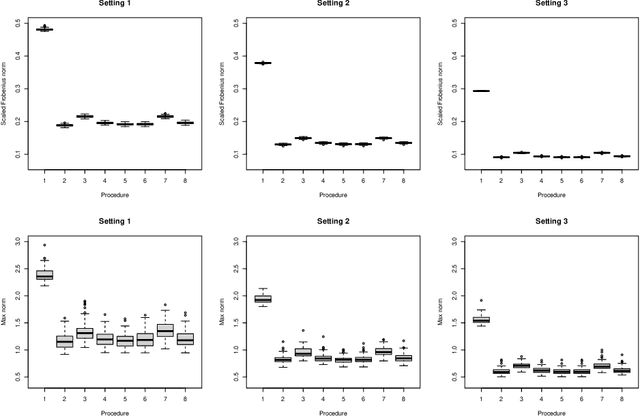

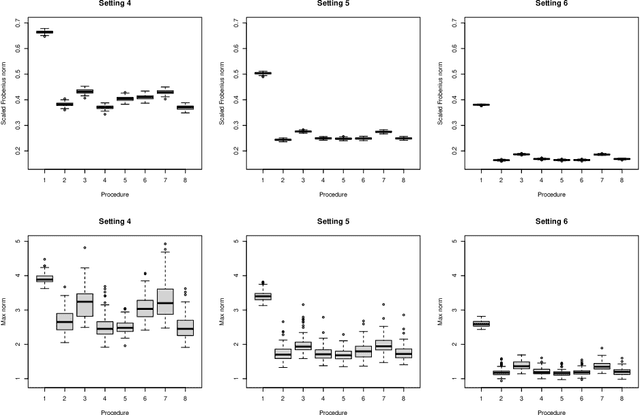
Matrix completion is a class of machine learning methods that concerns the prediction of missing entries in a partially observed matrix. This paper studies matrix completion for mixed data, i.e., data involving mixed types of variables (e.g., continuous, binary, ordinal). We formulate it as a low-rank matrix estimation problem under a general family of non-linear factor models and then propose entrywise consistent estimators for estimating the low-rank matrix. Tight probabilistic error bounds are derived for the proposed estimators. The proposed methods are evaluated by simulation studies and real-data applications for collaborative filtering and large-scale educational assessment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge