Bayesian Sparse Regression for Mixed Multi-Responses with Application to Runtime Metrics Prediction in Fog Manufacturing

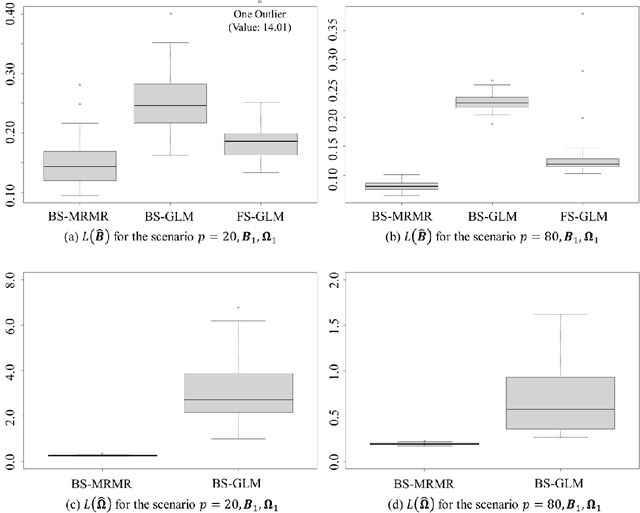
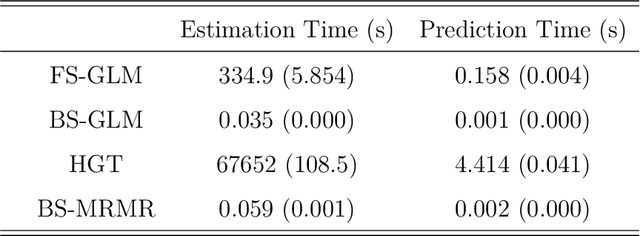
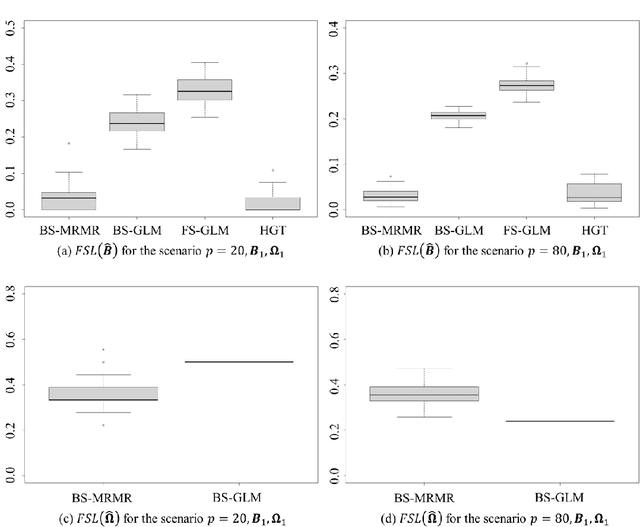
Fog manufacturing can greatly enhance traditional manufacturing systems through distributed Fog computation units, which are governed by predictive computational workload offloading methods under different Industrial Internet architectures. It is known that the predictive offloading methods highly depend on accurate prediction and uncertainty quantification of runtime performance metrics, containing multivariate mixed-type responses (i.e., continuous, counting, binary). In this work, we propose a Bayesian sparse regression for multivariate mixed responses to enhance the prediction of runtime performance metrics and to enable the statistical inferences. The proposed method considers both group and individual variable selection to jointly model the mixed types of runtime performance metrics. The conditional dependency among multiple responses is described by a graphical model using the precision matrix, where a spike-and-slab prior is used to enable the sparse estimation of the graph. The proposed method not only achieves accurate prediction, but also makes the predictive model more interpretable with statistical inferences on model parameters and prediction in the Fog manufacturing. A simulation study and a real case example in a Fog manufacturing are conducted to demonstrate the merits of the proposed model.

An Improved Modified Cholesky Decomposition Method for Inverse Covariance Matrix Estimation

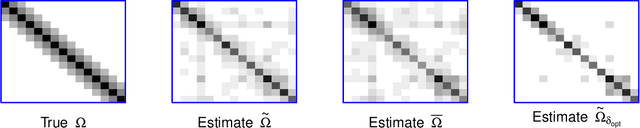
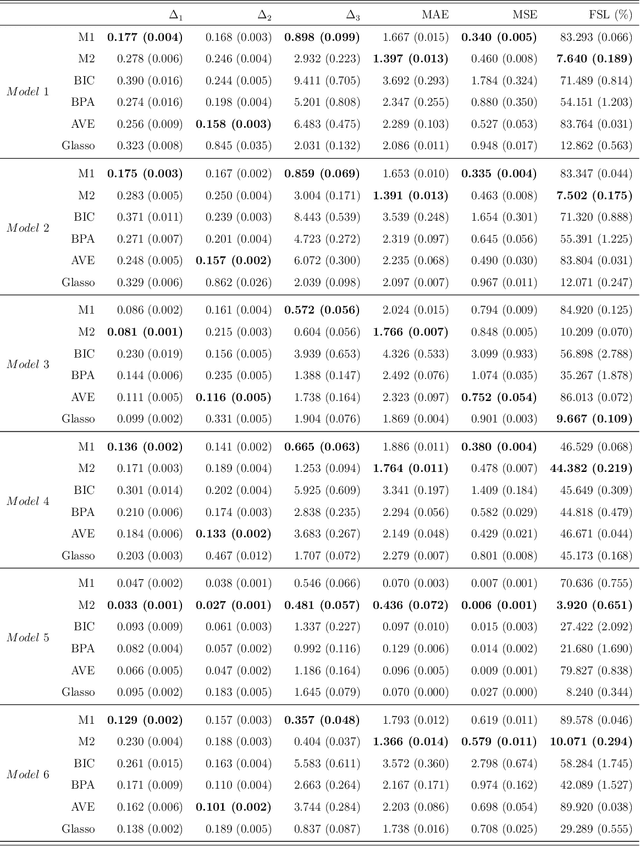
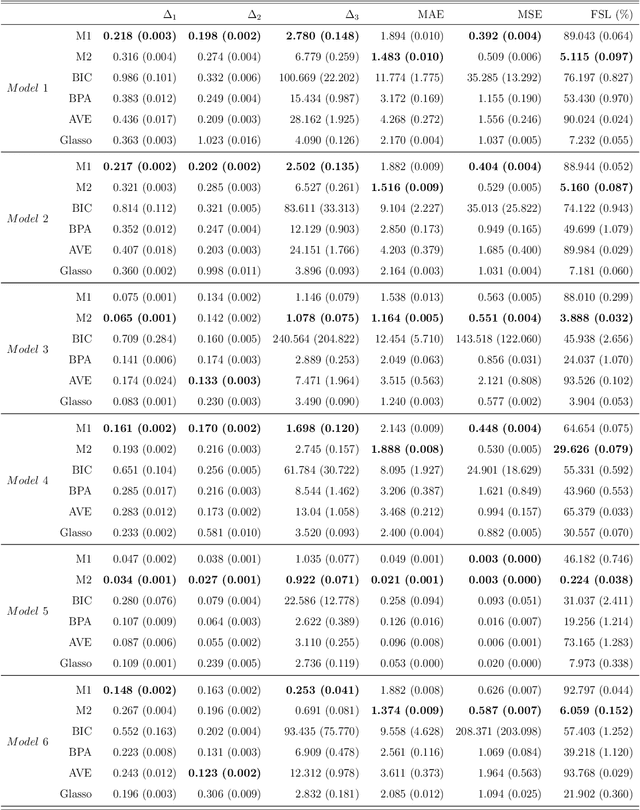
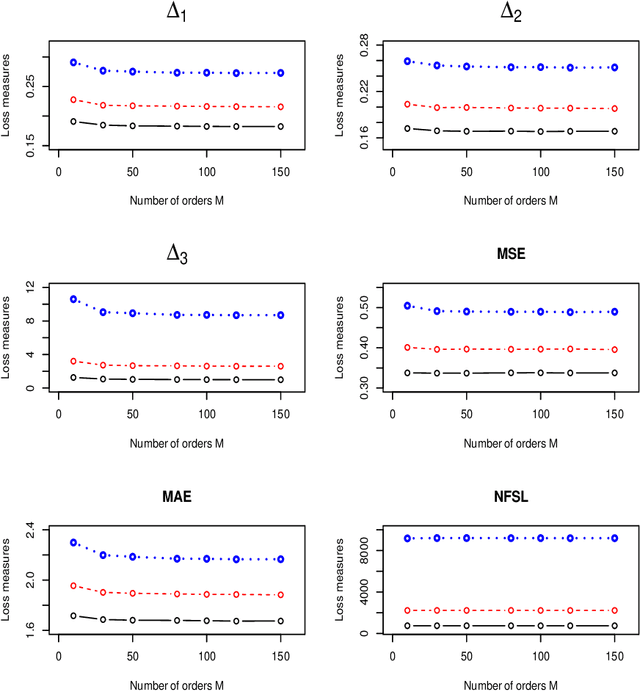
The modified Cholesky decomposition is commonly used for inverse covariance matrix estimation given a specified order of random variables. However, the order of variables is often not available or cannot be pre-determined. Hence, we propose a novel estimator to address the variable order issue in the modified Cholesky decomposition to estimate the sparse inverse covariance matrix. The key idea is to effectively combine a set of estimates obtained from multiple permutations of variable orders, and to efficiently encourage the sparse structure for the resultant estimate by the use of thresholding technique on the combined Cholesky factor matrix. The consistent property of the proposed estimate is established under some weak regularity conditions. Simulation studies show the superior performance of the proposed method in comparison with several existing approaches. We also apply the proposed method into the linear discriminant analysis for analyzing real-data examples for classification.