An Improved Modified Cholesky Decomposition Method for Inverse Covariance Matrix Estimation

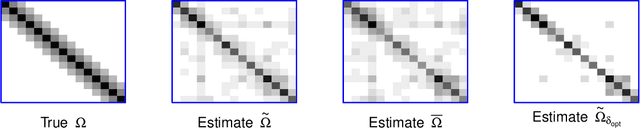
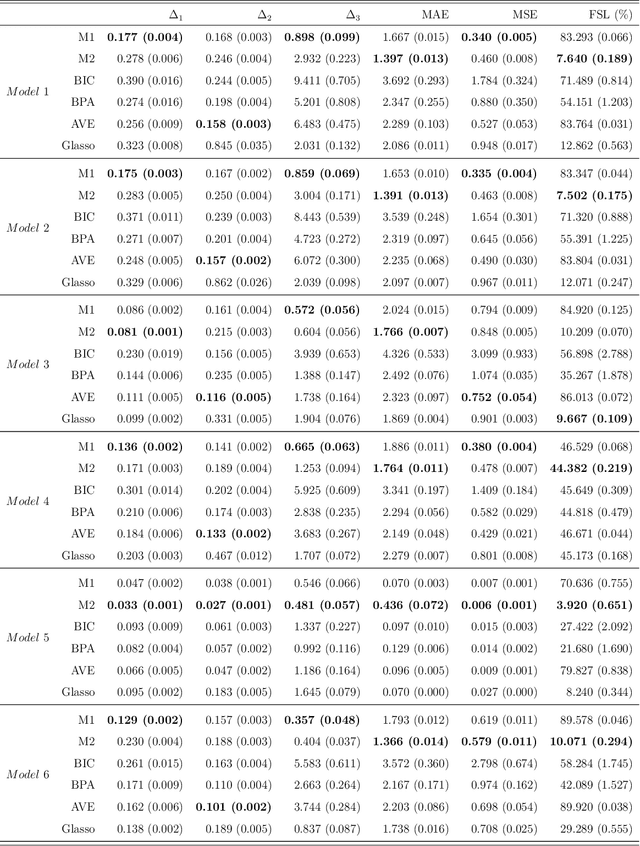
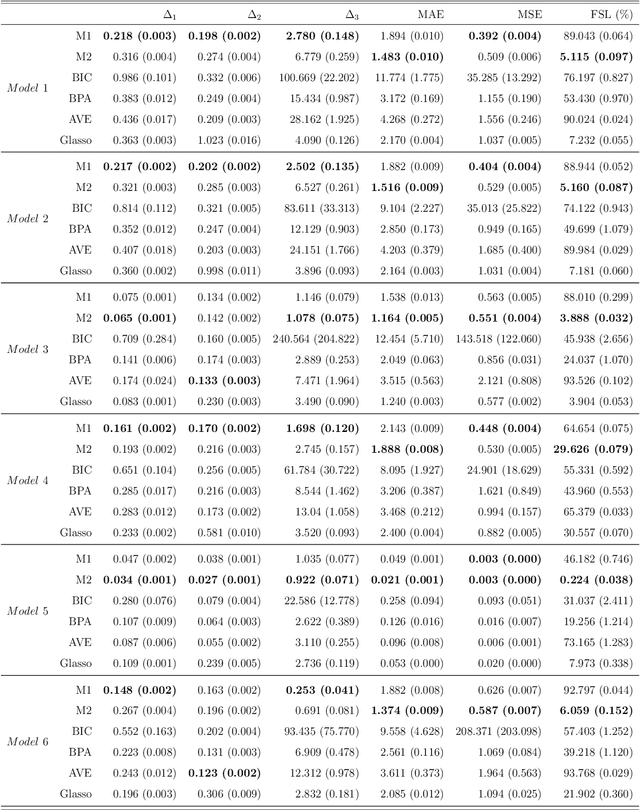
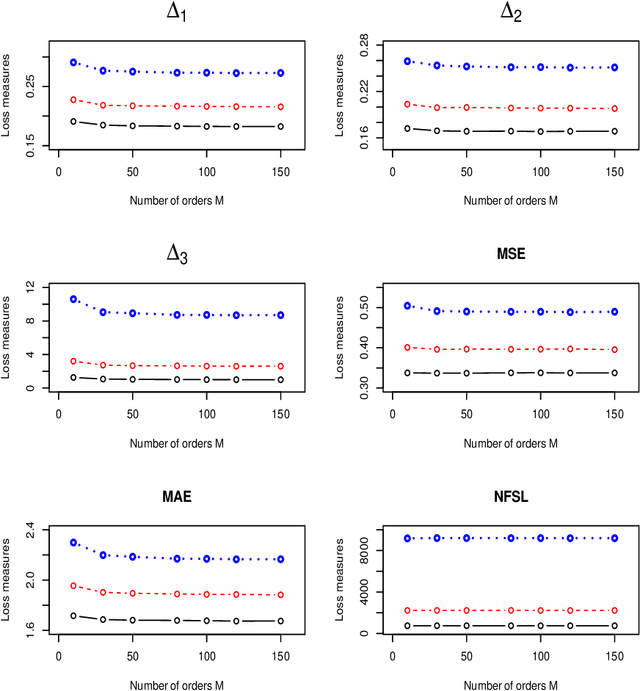
The modified Cholesky decomposition is commonly used for inverse covariance matrix estimation given a specified order of random variables. However, the order of variables is often not available or cannot be pre-determined. Hence, we propose a novel estimator to address the variable order issue in the modified Cholesky decomposition to estimate the sparse inverse covariance matrix. The key idea is to effectively combine a set of estimates obtained from multiple permutations of variable orders, and to efficiently encourage the sparse structure for the resultant estimate by the use of thresholding technique on the combined Cholesky factor matrix. The consistent property of the proposed estimate is established under some weak regularity conditions. Simulation studies show the superior performance of the proposed method in comparison with several existing approaches. We also apply the proposed method into the linear discriminant analysis for analyzing real-data examples for classification.