PolyLoss: A Polynomial Expansion Perspective of Classification Loss Functions

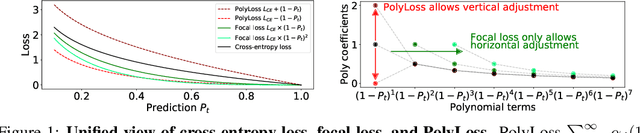
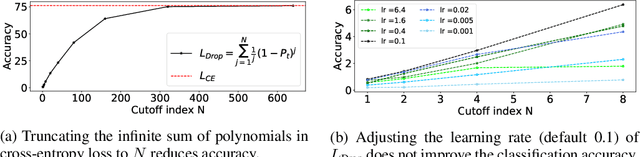
Cross-entropy loss and focal loss are the most common choices when training deep neural networks for classification problems. Generally speaking, however, a good loss function can take on much more flexible forms, and should be tailored for different tasks and datasets. Motivated by how functions can be approximated via Taylor expansion, we propose a simple framework, named PolyLoss, to view and design loss functions as a linear combination of polynomial functions. Our PolyLoss allows the importance of different polynomial bases to be easily adjusted depending on the targeting tasks and datasets, while naturally subsuming the aforementioned cross-entropy loss and focal loss as special cases. Extensive experimental results show that the optimal choice within the PolyLoss is indeed dependent on the task and dataset. Simply by introducing one extra hyperparameter and adding one line of code, our Poly-1 formulation outperforms the cross-entropy loss and focal loss on 2D image classification, instance segmentation, object detection, and 3D object detection tasks, sometimes by a large margin.

Research on the Multiple Feature Fusion Image Retrieval Algorithm based on Texture Feature and Rough Set Theory

Recently, we have witnessed the explosive growth of images with complex information and content. In order to effectively and precisely retrieve desired images from a large-scale image database with low time-consuming, we propose the multiple feature fusion image retrieval algorithm based on the texture feature and rough set theory in this paper. In contrast to the conventional approaches that only use the single feature or standard, we fuse the different features with operation of normalization. The rough set theory will assist us to enhance the robustness of retrieval system when facing with incomplete data warehouse. To enhance the texture extraction paradigm, we use the wavelet Gabor function that holds better robustness. In addition, from the perspectives of the internal and external normalization, we re-organize extracted feature with the better combination. The numerical experiment has verified general feasibility of our methodology. We enhance the overall accuracy compared with the other state-of-the-art algorithms.