IF equation: a feature extractor for high-concentration time-frequency representation

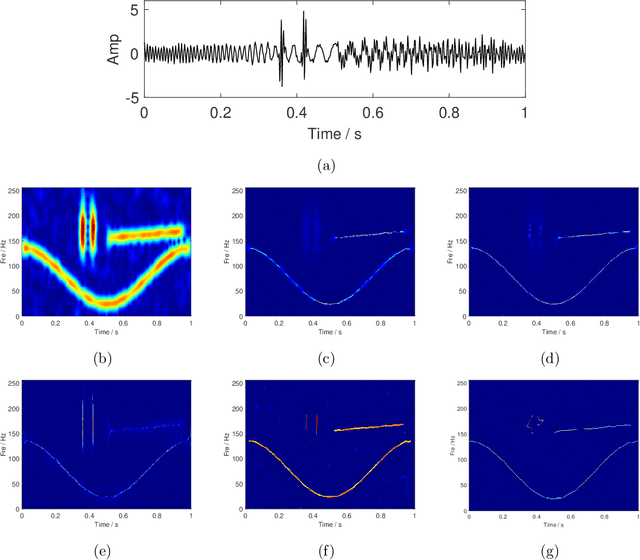
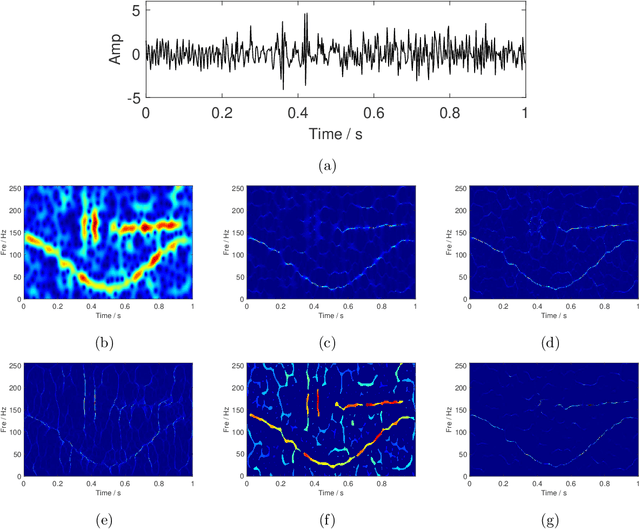
High-concentration time-frequency (TF) representation provides a valuable tool for characterizing multi-component non-stationary signals. In our previous work, we proposed using an instantaneous frequency (IF) equation to sharpen the TF distribution and its effectiveness has been verified in experiments. In this paper, we systematically discuss why the IF equation-based TF analysis methods work and how to use the IF equation to improve the TF sharpness. By theory analysis, many popular TF post-processing methods, such as the synchroextracting transform, the multi-synchrosqueezing transform, and the time extracting transform, fall into the IF equation-based category. A comparison of the IF equation-based method with the popular synchrosqueezing transform is made. Numerical examples of the theoretical derivations are presented to illustrate the performance of the proposed IF equation-based TF analysis method.

High-resolution chirplet transform: from parameters analysis to parameters combination

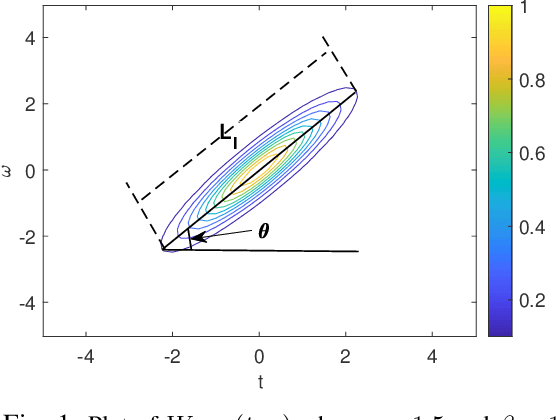
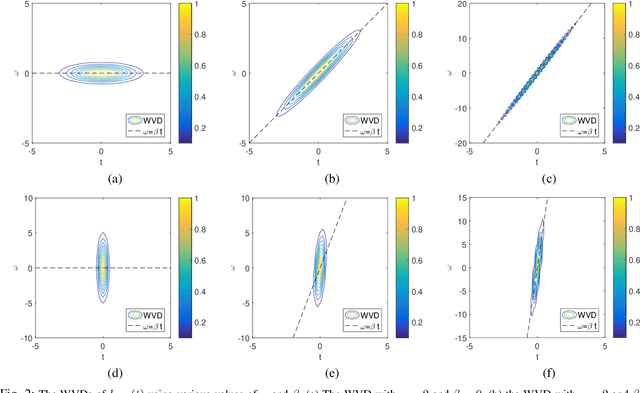
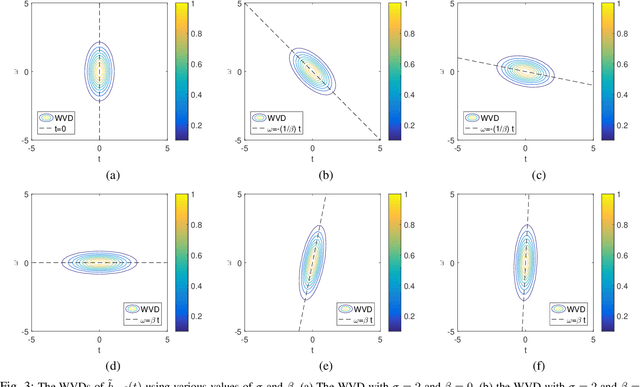
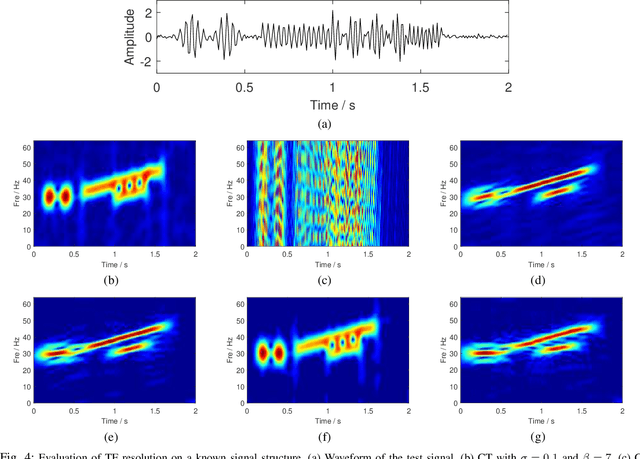
The standard chirplet transform (CT) with a chirp-modulated Gaussian window provides a valuable tool for analyzing linear chirp signals. The parameters present in the window determine the performance of CT and play a very important role in high-resolution time-frequency (TF) analysis. In this paper, we first give the window shape analysis of CT and compare it with the extension that employs a rotating Gaussian window by fractional Fourier transform. The given parameters analysis provides certain theoretical guidance for developing high-resolution CT. We then propose a multi-resolution chirplet transform (MrCT) by combining multiple CTs with different parameter combinations. These are combined geometrically to obtain an improved TF resolution by overcoming the limitations of any single representation of the CT. By deriving the combined instantaneous frequency equation, we further develop a high-concentration TF post-processing approach to improve the readability of the MrCT. Numerical experiments on simulated and real signals verify its effectiveness.