Xiangdong Qiu
Wide-Beam Array Antenna Power Gain Maximization via ADMM Framework
Apr 21, 2021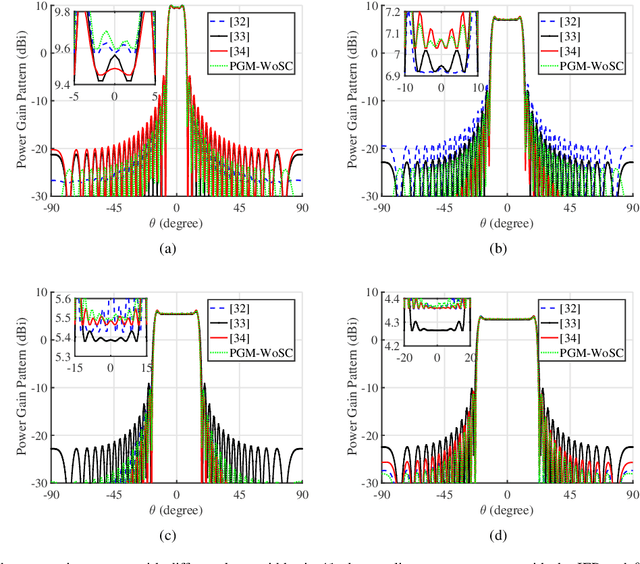
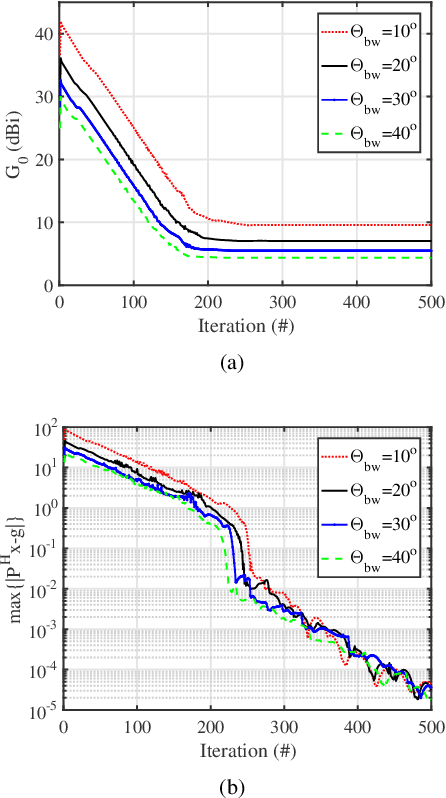
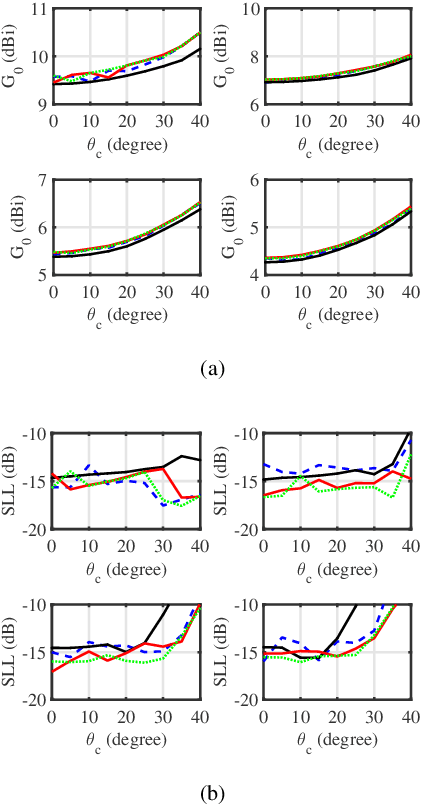
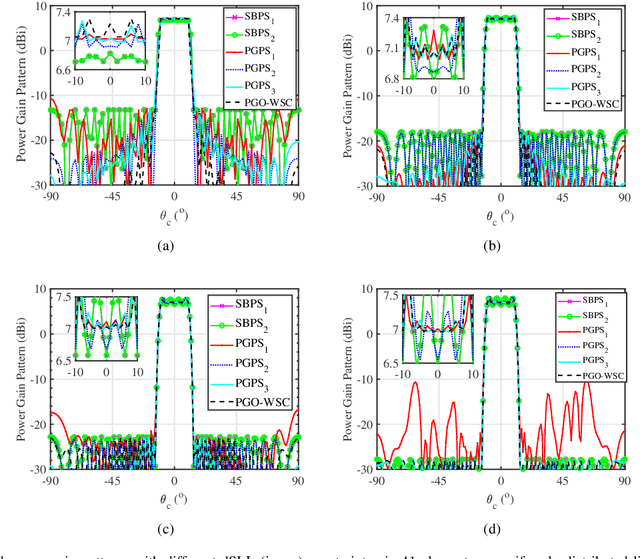
Abstract:This paper proposes two algorithms to maximize the minimum array power gain in a wide-beam mainlobe by solving the power gain pattern synthesis (PGPS) problem with and without sidelobe constraints. Firstly, the nonconvex PGPS problem is transformed into a nonconvex linear inequality optimization problem and then converted to an augmented Lagrangian problem by introducing auxiliary variables via the Alternating Direction Method of Multipliers (ADMM) framework. Next,the original intractable problem is converted into a series of nonconvex and convex subproblems. The nonconvex subproblems are solved by dividing their solution space into a finite set of smaller ones, in which the solution would be obtained pseudoanalytically. In such a way, the proposed algorithms are superior to the existing PGPS-based ones as their convergence can be theoretically guaranteed with a lower computational burden. Numerical examples with both isotropic element pattern (IEP) and active element pattern (AEP) arrays are simulated to show the effectiveness and superiority of the proposed algorithms by comparing with the related existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge