Artificial-Intelligence-Based Design for Circuit Parameters of Power Converters

Parameter design is significant in ensuring a satisfactory holistic performance of power converters. Generally, circuit parameter design for power converters consists of two processes: analysis and deduction process and optimization process. The existing approaches for parameter design consist of two types: traditional approach and computer-aided optimization (CAO) approach. In the traditional approaches, heavy human-dependence is required. Even though the emerging CAO approaches automate the optimization process, they still require manual analysis and deduction process. To mitigate human-dependence for the sake of high accuracy and easy implementation, an artificial-intelligence-based design (AI-D) approach is proposed in this article for the parameter design of power converters. In the proposed AI-D approach, to achieve automation in the analysis and deduction process, simulation tools and batch-normalization neural network (BN-NN) are adopted to build data-driven models for the optimization objectives and design constraints. Besides, to achieve automation in the optimization process, genetic algorithm is used to search for optimal design results. The proposed AI-D approach is validated in the circuit parameter design of the synchronous buck converter in the 48 to 12 V accessory-load power supply system in electric vehicle. The design case of an efficiency-optimal synchronous buck converter with constraints in volume, voltage ripple, and current ripple is provided. In the end of this article, feasibility and accuracy of the proposed AI-D approach have been validated by hardware experiments.

A Generative deep learning approach for shape recognition of arbitrary objects from phaseless acoustic scattering data

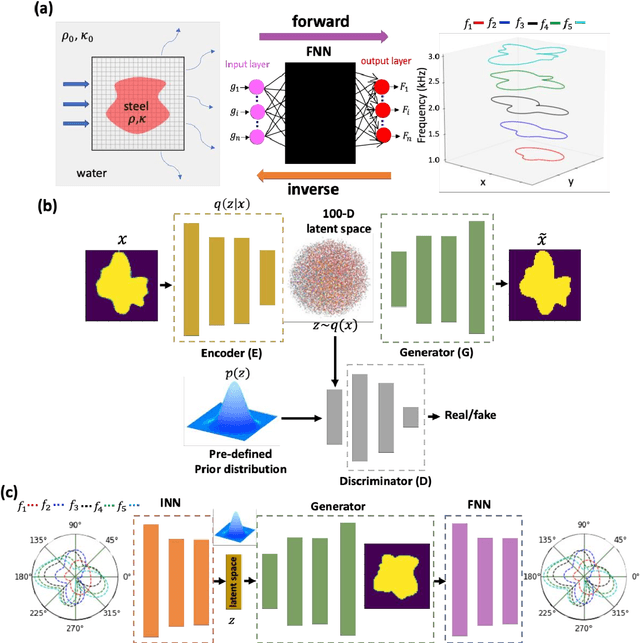
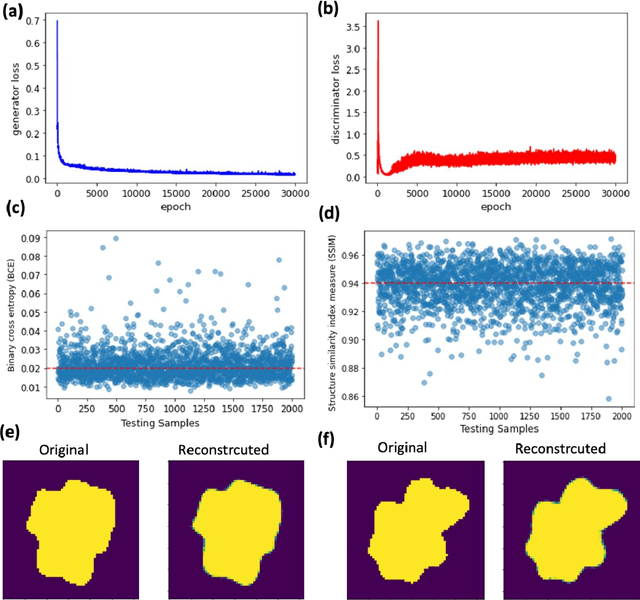
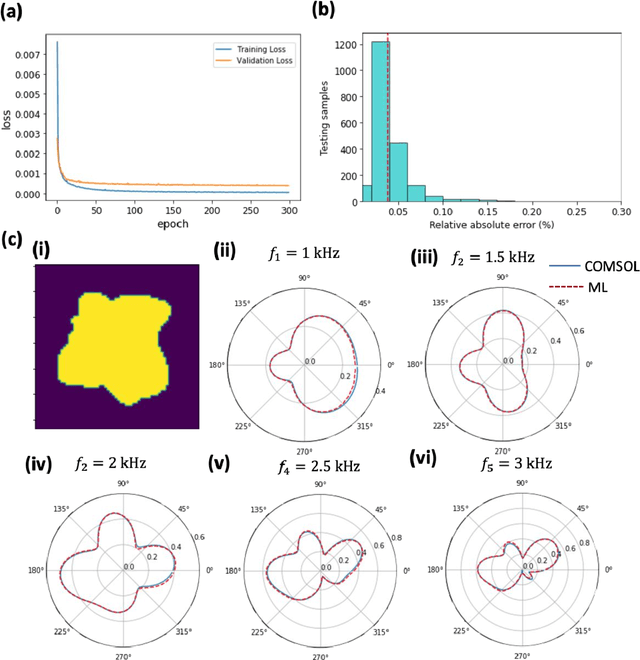
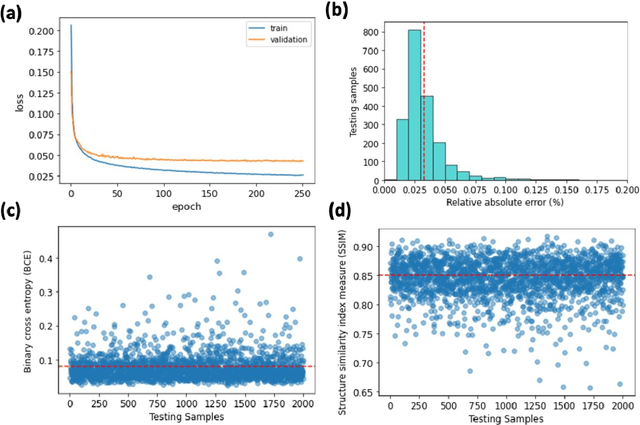
We propose and demonstrate a generative deep learning approach for the shape recognition of an arbitrary object from its acoustic scattering properties. The strategy exploits deep neural networks to learn the mapping between the latent space of a two-dimensional acoustic object and the far-field scattering amplitudes. A neural network is designed as an Adversarial autoencoder and trained via unsupervised learning to determine the latent space of the acoustic object. Important structural features of the object are embedded in lower-dimensional latent space which supports the modeling of a shape generator and accelerates the learning in the inverse design process.The proposed inverse design uses the variational inference approach with encoder and decoder-like architecture where the decoder is composed of two pretrained neural networks, the generator and the forward model. The data-driven framework finds an accurate solution to the ill-posed inverse scattering problem, where non-unique solution space is overcome by the multifrequency phaseless far-field patterns. This inverse method is a powerful design tool that does not require complex analytical calculation and opens up new avenues for practical realization, automatic recognition of arbitrary shaped submarines or large fish, and other underwater applications.

Machine learning for knowledge acquisition and accelerated inverse-design for non-Hermitian systems

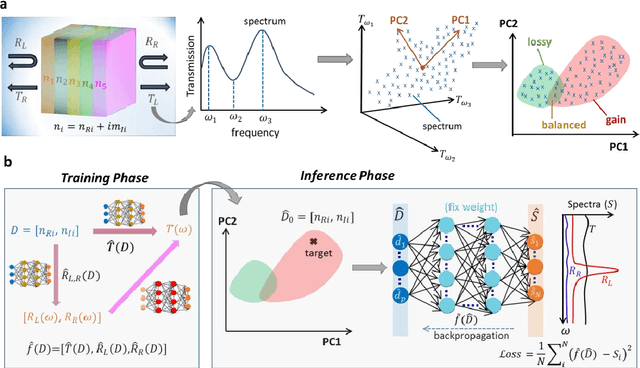
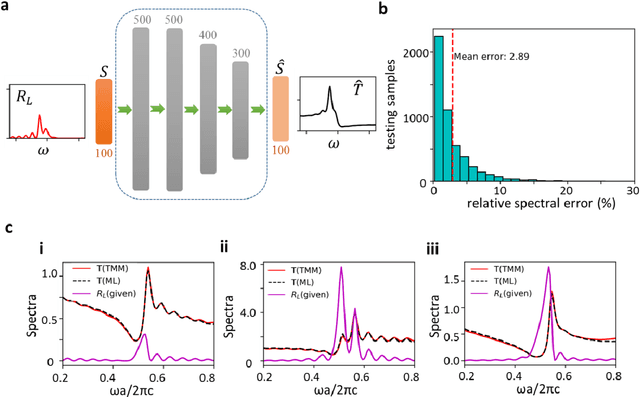
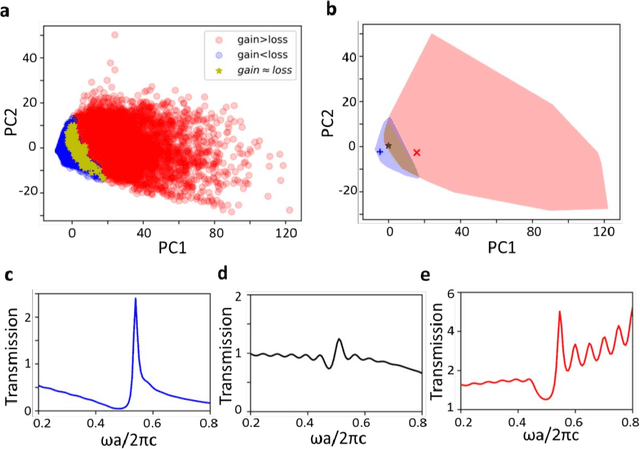
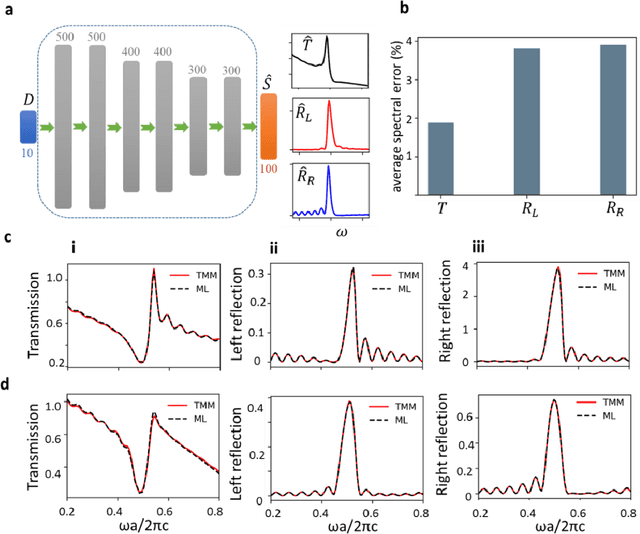
Non-Hermitian systems offer new platforms for unusual physical properties that can be flexibly manipulated by redistribution of the real and imaginary parts of refractive indices, whose presence breaks conventional wave propagation symmetries, leading to asymmetric reflection and symmetric transmission with respect to the wave propagation direction. Here, we use supervised and unsupervised learning techniques for knowledge acquisition in non-Hermitian systems which accelerate the inverse design process. In particular, we construct a deep learning model that relates the transmission and asymmetric reflection in non-conservative settings and proposes sub-manifold learning to recognize non-Hermitian features from transmission spectra. The developed deep learning framework determines the feasibility of a desired spectral response for a given structure and uncovers the role of effective gain-loss parameters to tailor the spectral response. These findings pave the way for intelligent inverse design and shape our understanding of the physical mechanism in general non-Hermitian systems.

Picture Fuzzy Interactional Aggregation Operators via Strict Triangular Norms and Applications to Multi-Criteria Decision Making

The picture fuzzy set, characterized by three membership degrees, is a helpful tool for multi-criteria decision making (MCDM). This paper investigates the structure of the closed operational laws in the picture fuzzy numbers (PFNs) and proposes efficient picture fuzzy MCDM methods. We first introduce an admissible order for PFNs and prove that all PFNs form a complete lattice under this order. Then, we give some specific examples to show the non-closeness of some existing picture fuzzy aggregation operators. To ensure the closeness of the operational laws in PFNs, we construct a new class of picture fuzzy operators based on strict triangular norms, which consider the interaction between the positive degrees (negative degrees) and the neutral degrees. Based on these new operators, we obtain the picture fuzzy interactional weighted average (PFIWA) operator and the picture fuzzy interactional weighted geometric (PFIWG) operator. They are proved to be monotonous, idempotent, bounded, shift-invariant, and homogeneous. We also establish a novel MCDM method under the picture fuzzy environment applying PFIWA and PFIWG operators. Furthermore, we present an illustrative example for a clear understanding of our method. We also give the comparative analysis among the operators induced by six classes of famous triangular norms.