Applying Eigencontours to PolarMask-Based Instance Segmentation

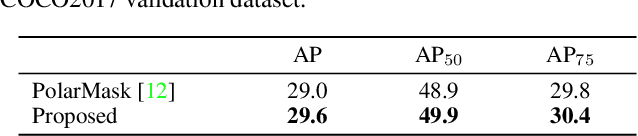
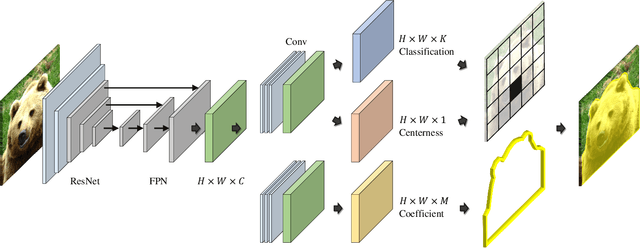
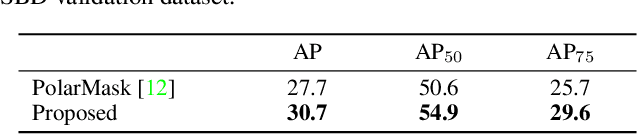
Eigencontours are the first data-driven contour descriptors based on singular value decomposition. Based on the implementation of ESE-Seg, eigencontours were applied to the instance segmentation task successfully. In this report, we incorporate eigencontours into the PolarMask network for instance segmentation. Experimental results demonstrate that the proposed algorithm yields better results than PolarMask on two instance segmentation datasets of COCO2017 and SBD. Also, we analyze the characteristics of eigencontours qualitatively. Our codes are available at https://github.com/dnjs3594/Eigencontours.

Eigenlanes: Data-Driven Lane Descriptors for Structurally Diverse Lanes

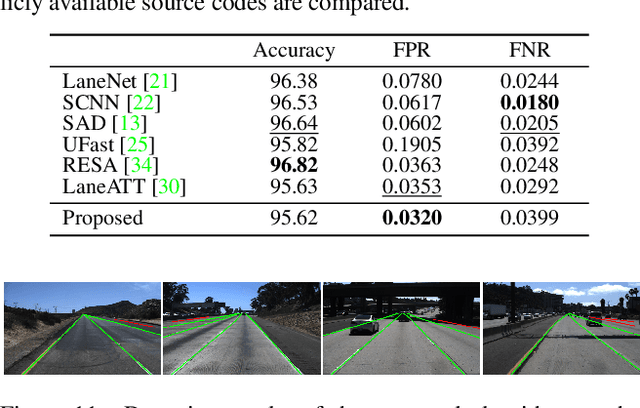
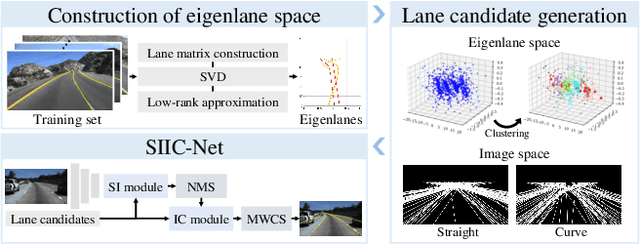
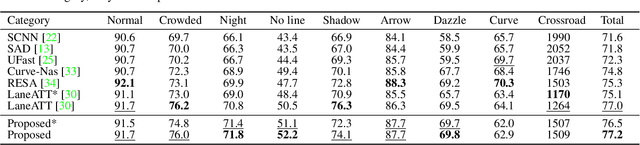
A novel algorithm to detect road lanes in the eigenlane space is proposed in this paper. First, we introduce the notion of eigenlanes, which are data-driven descriptors for structurally diverse lanes, including curved, as well as straight, lanes. To obtain eigenlanes, we perform the best rank-M approximation of a lane matrix containing all lanes in a training set. Second, we generate a set of lane candidates by clustering the training lanes in the eigenlane space. Third, using the lane candidates, we determine an optimal set of lanes by developing an anchor-based detection network, called SIIC-Net. Experimental results demonstrate that the proposed algorithm provides excellent detection performance for structurally diverse lanes. Our codes are available at https://github.com/dongkwonjin/Eigenlanes.

Eigencontours: Novel Contour Descriptors Based on Low-Rank Approximation

Novel contour descriptors, called eigencontours, based on low-rank approximation are proposed in this paper. First, we construct a contour matrix containing all object boundaries in a training set. Second, we decompose the contour matrix into eigencontours via the best rank-M approximation. Third, we represent an object boundary by a linear combination of the M eigencontours. We also incorporate the eigencontours into an instance segmentation framework. Experimental results demonstrate that the proposed eigencontours can represent object boundaries more effectively and more efficiently than existing descriptors in a low-dimensional space. Furthermore, the proposed algorithm yields meaningful performances on instance segmentation datasets.

Harmonious Semantic Line Detection via Maximal Weight Clique Selection

A novel algorithm to detect an optimal set of semantic lines is proposed in this work. We develop two networks: selection network (S-Net) and harmonization network (H-Net). First, S-Net computes the probabilities and offsets of line candidates. Second, we filter out irrelevant lines through a selection-and-removal process. Third, we construct a complete graph, whose edge weights are computed by H-Net. Finally, we determine a maximal weight clique representing an optimal set of semantic lines. Moreover, to assess the overall harmony of detected lines, we propose a novel metric, called HIoU. Experimental results demonstrate that the proposed algorithm can detect harmonious semantic lines effectively and efficiently. Our codes are available at https://github.com/dongkwonjin/Semantic-Line-MWCS.