William R. Sickinger
Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time
Jun 12, 2020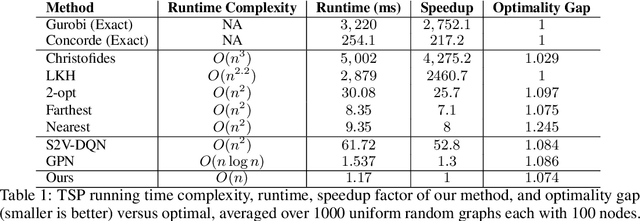
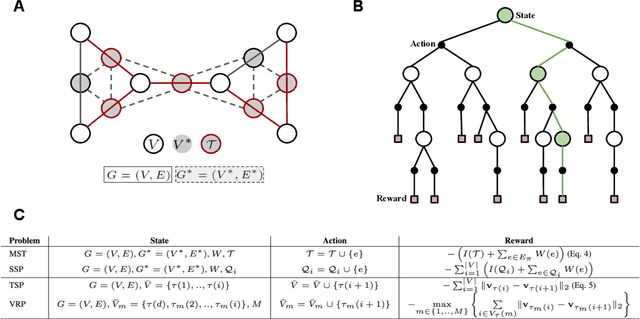
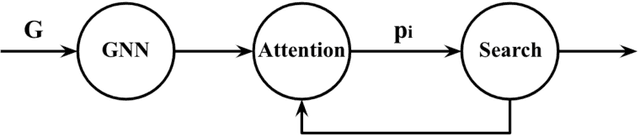
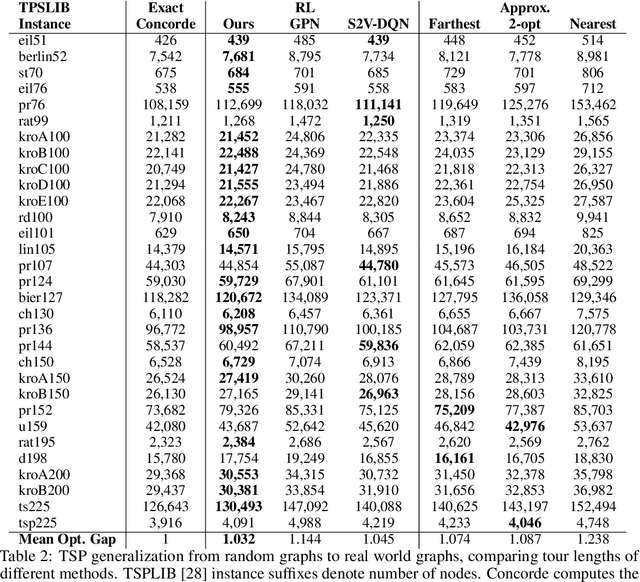
Abstract:Combinatorial optimization algorithms for graph problems are usually designed afresh for each new problem with careful attention by an expert to the problem structure. In this work, we develop a new framework to solve any combinatorial optimization problem over graphs that can be formulated as a single player game defined by states, actions, and rewards, including minimum spanning tree, shortest paths, traveling salesman problem, and vehicle routing problem, without expert knowledge. Our method trains a graph neural network using reinforcement learning on an unlabeled training set of graphs. The trained network then outputs approximate solutions to new graph instances in linear running time. In contrast, previous approximation algorithms or heuristics tailored to NP-hard problems on graphs generally have at least quadratic running time. We demonstrate the applicability of our approach on both polynomial and NP-hard problems with optimality gaps close to 1, and show that our method is able to generalize well: (i) from training on small graphs to testing on large graphs; (ii) from training on random graphs of one type to testing on random graphs of another type; and (iii) from training on random graphs to running on real world graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge