Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time

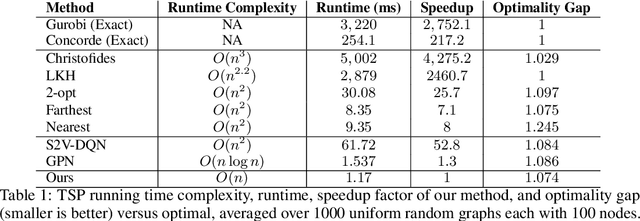
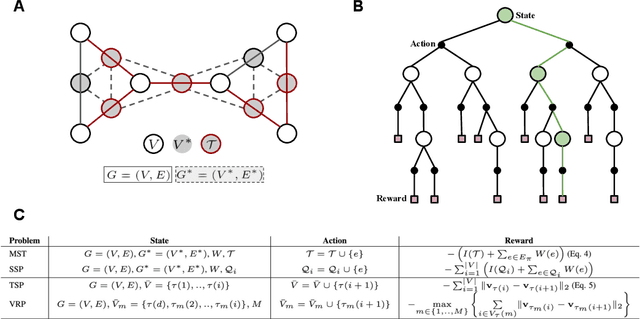
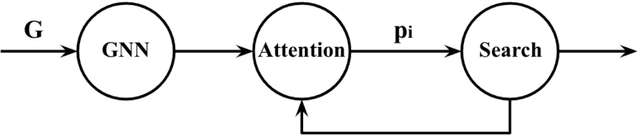
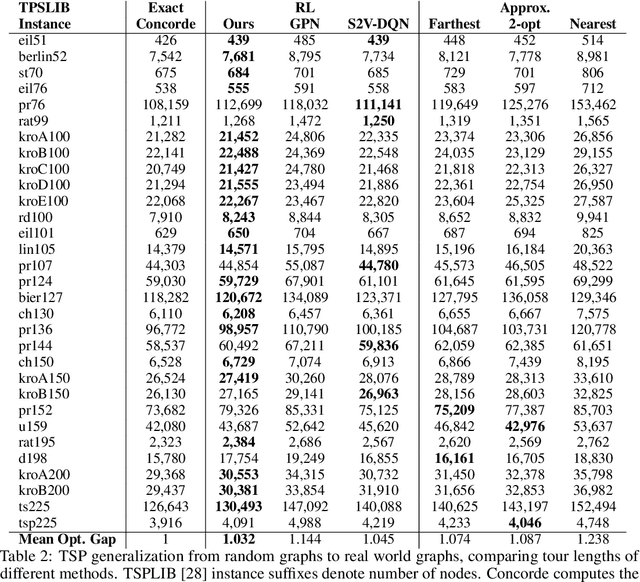
Combinatorial optimization algorithms for graph problems are usually designed afresh for each new problem with careful attention by an expert to the problem structure. In this work, we develop a new framework to solve any combinatorial optimization problem over graphs that can be formulated as a single player game defined by states, actions, and rewards, including minimum spanning tree, shortest paths, traveling salesman problem, and vehicle routing problem, without expert knowledge. Our method trains a graph neural network using reinforcement learning on an unlabeled training set of graphs. The trained network then outputs approximate solutions to new graph instances in linear running time. In contrast, previous approximation algorithms or heuristics tailored to NP-hard problems on graphs generally have at least quadratic running time. We demonstrate the applicability of our approach on both polynomial and NP-hard problems with optimality gaps close to 1, and show that our method is able to generalize well: (i) from training on small graphs to testing on large graphs; (ii) from training on random graphs of one type to testing on random graphs of another type; and (iii) from training on random graphs to running on real world graphs.

Combinatorial Optimization by Graph Pointer Networks and Hierarchical Reinforcement Learning

In this work, we introduce Graph Pointer Networks (GPNs) trained using reinforcement learning (RL) for tackling the traveling salesman problem (TSP). GPNs build upon Pointer Networks by introducing a graph embedding layer on the input, which captures relationships between nodes. Furthermore, to approximate solutions to constrained combinatorial optimization problems such as the TSP with time windows, we train hierarchical GPNs (HGPNs) using RL, which learns a hierarchical policy to find an optimal city permutation under constraints. Each layer of the hierarchy is designed with a separate reward function, resulting in stable training. Our results demonstrate that GPNs trained on small-scale TSP50/100 problems generalize well to larger-scale TSP500/1000 problems, with shorter tour lengths and faster computational times. We verify that for constrained TSP problems such as the TSP with time windows, the feasible solutions found via hierarchical RL training outperform previous baselines. In the spirit of reproducible research we make our data, models, and code publicly available.