Mixtures of Gaussians and Minimum Relative Entropy Techniques for Modeling Continuous Uncertainties

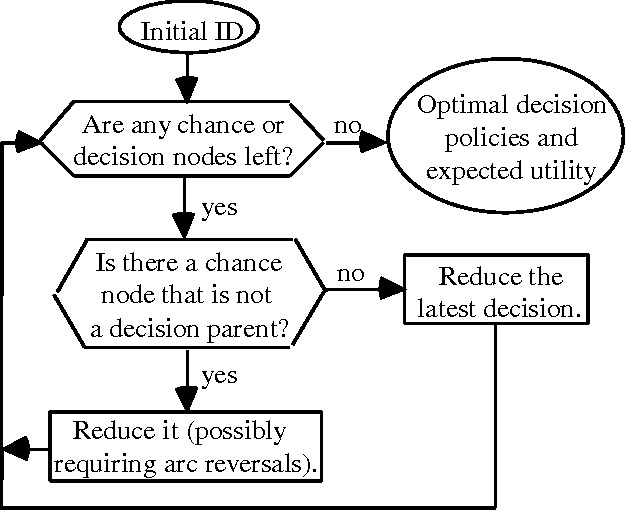
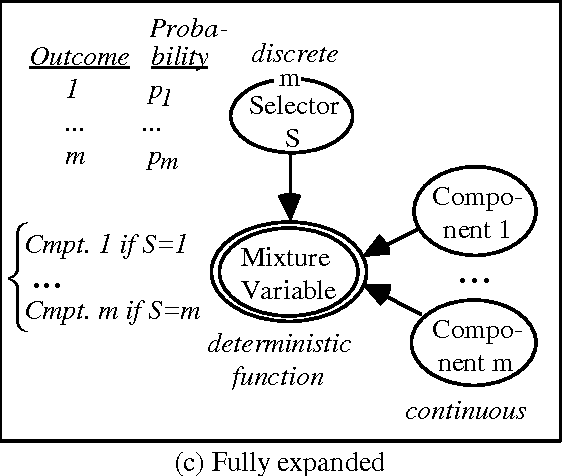
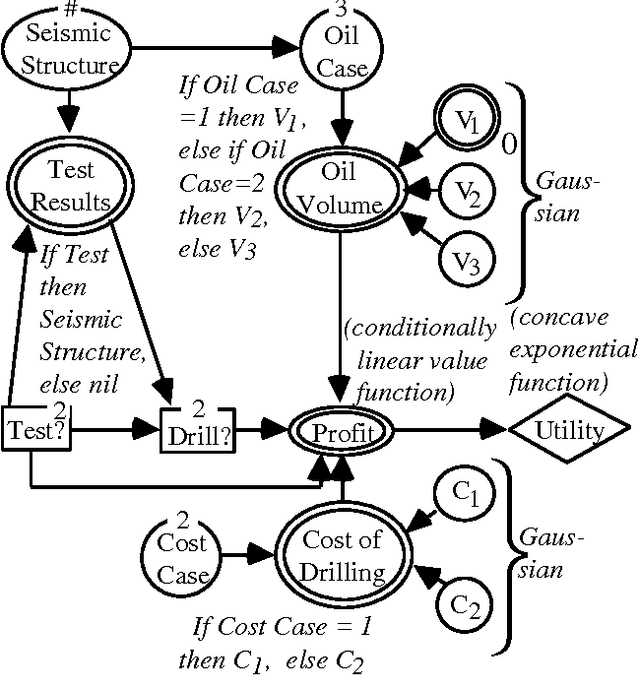
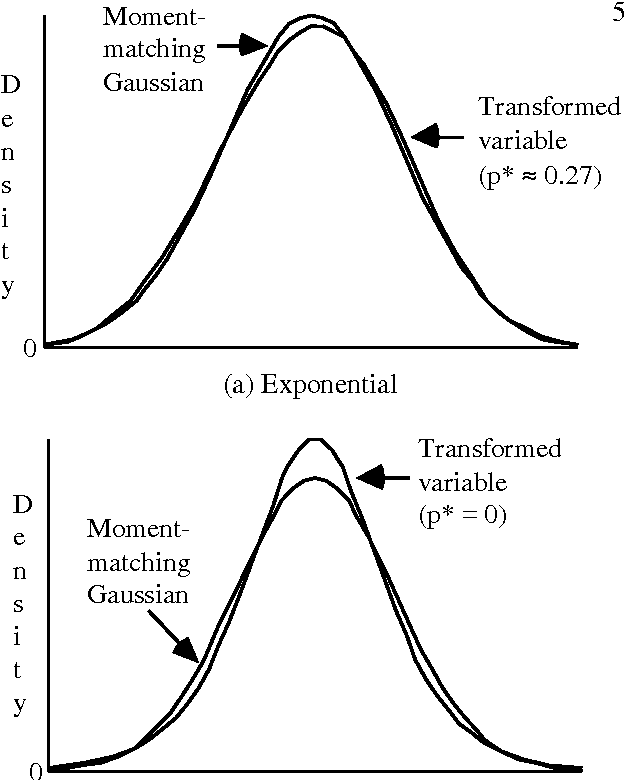
Problems of probabilistic inference and decision making under uncertainty commonly involve continuous random variables. Often these are discretized to a few points, to simplify assessments and computations. An alternative approximation is to fit analytically tractable continuous probability distributions. This approach has potential simplicity and accuracy advantages, especially if variables can be transformed first. This paper shows how a minimum relative entropy criterion can drive both transformation and fitting, illustrating with a power and logarithm family of transformations and mixtures of Gaussian (normal) distributions, which allow use of efficient influence diagram methods. The fitting procedure in this case is the well-known EM algorithm. The selection of the number of components in a fitted mixture distribution is automated with an objective that trades off accuracy and computational cost.

Three Approaches to Probability Model Selection

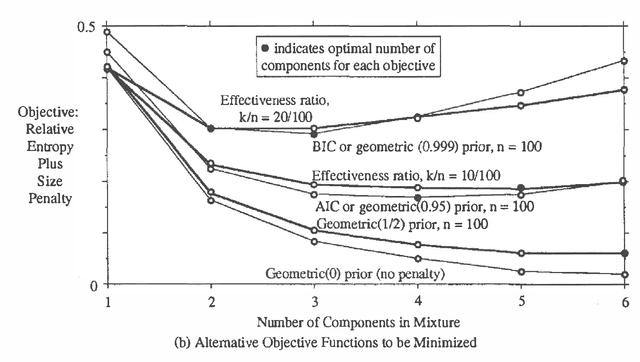
This paper compares three approaches to the problem of selecting among probability models to fit data (1) use of statistical criteria such as Akaike's information criterion and Schwarz's "Bayesian information criterion," (2) maximization of the posterior probability of the model, and (3) maximization of an effectiveness ratio? trading off accuracy and computational cost. The unifying characteristic of the approaches is that all can be viewed as maximizing a penalized likelihood function. The second approach with suitable prior distributions has been shown to reduce to the first. This paper shows that the third approach reduces to the second for a particular form of the effectiveness ratio, and illustrates all three approaches with the problem of selecting the number of components in a mixture of Gaussian distributions. Unlike the first two approaches, the third can be used even when the candidate models are chosen for computational efficiency, without regard to physical interpretation, so that the likelihood and the prior distribution over models cannot be interpreted literally. As the most general and computationally oriented of the approaches, it is especially useful for artificial intelligence applications.

Probabilistic Constraint Satisfaction with Non-Gaussian Noise

We have previously reported a Bayesian algorithm for determining the coordinates of points in three-dimensional space from uncertain constraints. This method is useful in the determination of biological molecular structure. It is limited, however, by the requirement that the uncertainty in the constraints be normally distributed. In this paper, we present an extension of the original algorithm that allows constraint uncertainty to be represented as a mixture of Gaussians, and thereby allows arbitrary constraint distributions. We illustrate the performance of this algorithm on a problem drawn from the domain of molecular structure determination, in which a multicomponent constraint representation produces a much more accurate solution than the old single component mechanism. The new mechanism uses mixture distributions to decompose the problem into a set of independent problems with unimodal constraint uncertainty. The results of the unimodal subproblems are periodically recombined using Bayes' law, to avoid combinatorial explosion. The new algorithm is particularly suited for parallel implementation.