Three Approaches to Probability Model Selection
Paper and Code
Feb 27, 2013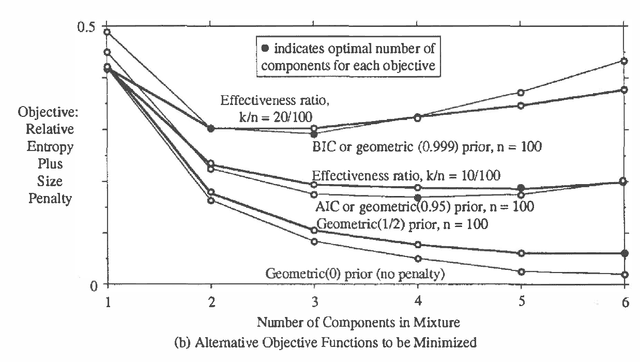
This paper compares three approaches to the problem of selecting among probability models to fit data (1) use of statistical criteria such as Akaike's information criterion and Schwarz's "Bayesian information criterion," (2) maximization of the posterior probability of the model, and (3) maximization of an effectiveness ratio? trading off accuracy and computational cost. The unifying characteristic of the approaches is that all can be viewed as maximizing a penalized likelihood function. The second approach with suitable prior distributions has been shown to reduce to the first. This paper shows that the third approach reduces to the second for a particular form of the effectiveness ratio, and illustrates all three approaches with the problem of selecting the number of components in a mixture of Gaussian distributions. Unlike the first two approaches, the third can be used even when the candidate models are chosen for computational efficiency, without regard to physical interpretation, so that the likelihood and the prior distribution over models cannot be interpreted literally. As the most general and computationally oriented of the approaches, it is especially useful for artificial intelligence applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge