A Decision-Based View of Causality

Most traditional models of uncertainty have focused on the associational relationship among variables as captured by conditional dependence. In order to successfully manage intelligent systems for decision making, however, we must be able to predict the effects of actions. In this paper, we attempt to unite two branches of research that address such predictions: causal modeling and decision analysis. First, we provide a definition of causal dependence in decision-analytic terms, which we derive from consequences of causal dependence cited in the literature. Using this definition, we show how causal dependence can be represented within an influence diagram. In particular, we identify two inadequacies of an ordinary influence diagram as a representation for cause. We introduce a special class of influence diagrams, called causal influence diagrams, which corrects one of these problems, and identify situations where the other inadequacy can be eliminated. In addition, we describe the relationships between Howard Canonical Form and existing graphical representations of cause.

A Definition and Graphical Representation for Causality

We present a precise definition of cause and effect in terms of a fundamental notion called unresponsiveness. Our definition is based on Savage's (1954) formulation of decision theory and departs from the traditional view of causation in that our causal assertions are made relative to a set of decisions. An important consequence of this departure is that we can reason about cause locally, not requiring a causal explanation for every dependency. Such local reasoning can be beneficial because it may not be necessary to determine whether a particular dependency is causal to make a decision. Also in this paper, we examine the graphical encoding of causal relationships. We show that influence diagrams in canonical form are an accurate and efficient representation of causal relationships. In addition, we establish a correspondence between canonical form and Pearl's causal theory.

Approximate Kalman Filter Q-Learning for Continuous State-Space MDPs

We seek to learn an effective policy for a Markov Decision Process (MDP) with continuous states via Q-Learning. Given a set of basis functions over state action pairs we search for a corresponding set of linear weights that minimizes the mean Bellman residual. Our algorithm uses a Kalman filter model to estimate those weights and we have developed a simpler approximate Kalman filter model that outperforms the current state of the art projected TD-Learning methods on several standard benchmark problems.

Intelligent Probabilistic Inference

The analysis of practical probabilistic models on the computer demands a convenient representation for the available knowledge and an efficient algorithm to perform inference. An appealing representation is the influence diagram, a network that makes explicit the random variables in a model and their probabilistic dependencies. Recent advances have developed solution procedures based on the influence diagram. In this paper, we examine the fundamental properties that underlie those techniques, and the information about the probabilistic structure that is available in the influence diagram representation. The influence diagram is a convenient representation for computer processing while also being clear and non-mathematical. It displays probabilistic dependence precisely, in a way that is intuitive for decision makers and experts to understand and communicate. As a result, the same influence diagram can be used to build, assess and analyze a model, facilitating changes in the formulation and feedback from sensitivity analysis. The goal in this paper is to determine arbitrary conditional probability distributions from a given probabilistic model. Given qualitative information about the dependence of the random variables in the model we can, for a specific conditional expression, specify precisely what quantitative information we need to be able to determine the desired conditional probability distribution. It is also shown how we can find that probability distribution by performing operations locally, that is, over subspaces of the joint distribution. In this way, we can exploit the conditional independence present in the model to avoid having to construct or manipulate the full joint distribution. These results are extended to include maximal processing when the information available is incomplete, and optimal decision making in an uncertain environment. Influence diagrams as a computer-aided modeling tool were developed by Miller, Merkofer, and Howard [5] and extended by Howard and Matheson [2]. Good descriptions of how to use them in modeling are in Owen [7] and Howard and Matheson [2]. The notion of solving a decision problem through influence diagrams was examined by Olmsted [6] and such an algorithm was developed by Shachter [8]. The latter paper also shows how influence diagrams can be used to perform a variety of sensitivity analyses. This paper extends those results by developing a theory of the properties of the diagram that are used by the algorithm, and the information needed to solve arbitrary probability inference problems. Section 2 develops the notation and the framework for the paper and the relationship between influence diagrams and joint probability distributions. The general probabilistic inference problem is posed in Section 3. In Section 4 the transformations on the diagram are developed and then put together into a solution procedure in Section 5. In Section 6, this procedure is used to calculate the information requirement to solve an inference problem and the maximal processing that can be performed with incomplete information. Section 7 contains a summary of results.

DAVID: Influence Diagram Processing System for the Macintosh

Influence diagrams are a directed graph representation for uncertainties as probabilities. The graph distinguishes between those variables which are under the control of a decision maker (decisions, shown as rectangles) and those which are not (chances, shown as ovals), as well as explicitly denoting a goal for solution (value, shown as a rounded rectangle.

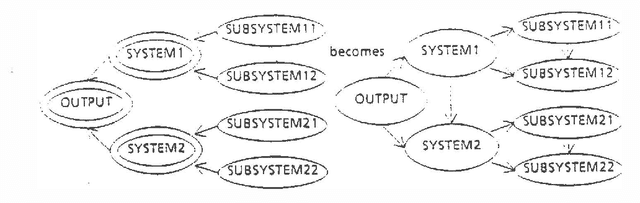
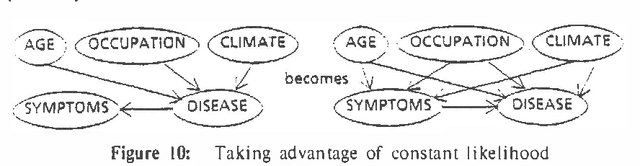
A Backwards View for Assessment

Much artificial intelligence research focuses on the problem of deducing the validity of unobservable propositions or hypotheses from observable evidence.! Many of the knowledge representation techniques designed for this problem encode the relationship between evidence and hypothesis in a directed manner. Moreover, the direction in which evidence is stored is typically from evidence to hypothesis.

Efficient Inference on Generalized Fault Diagrams

The generalized fault diagram, a data structure for failure analysis based on the influence diagram, is defined. Unlike the fault tree, this structure allows for dependence among the basic events and replicated logical elements. A heuristic procedure is developed for efficient processing of these structures.

A Heuristic Bayesian Approach to Knowledge Acquisition: Application to Analysis of Tissue-Type Plasminogen Activator

This paper describes a heuristic Bayesian method for computing probability distributions from experimental data, based upon the multivariate normal form of the influence diagram. An example illustrates its use in medical technology assessment. This approach facilitates the integration of results from different studies, and permits a medical expert to make proper assessments without considerable statistical training.

A Linear Approximation Method for Probabilistic Inference

An approximation method is presented for probabilistic inference with continuous random variables. These problems can arise in many practical problems, in particular where there are "second order" probabilities. The approximation, based on the Gaussian influence diagram, iterates over linear approximations to the inference problem.

Simulation Approaches to General Probabilistic Inference on Belief Networks

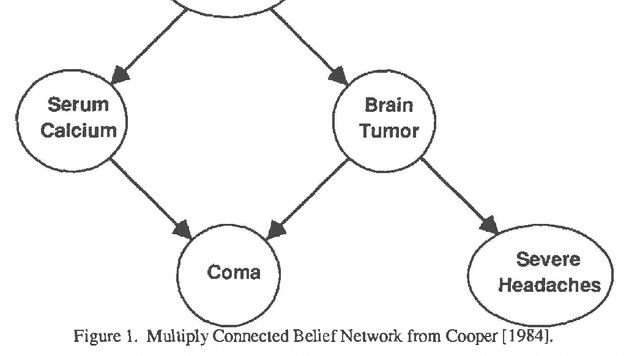
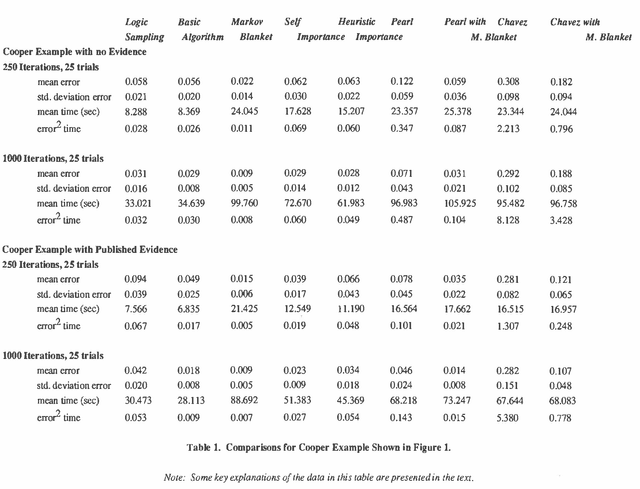
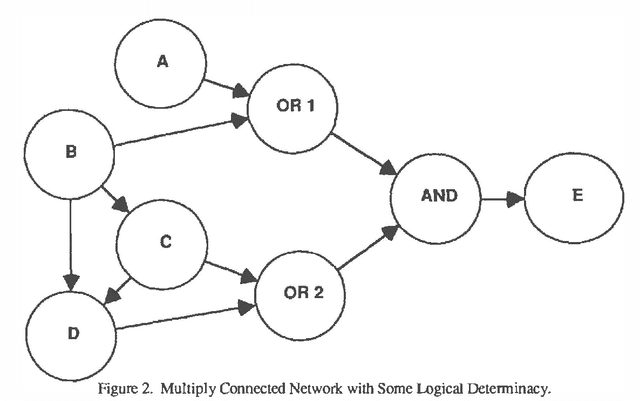
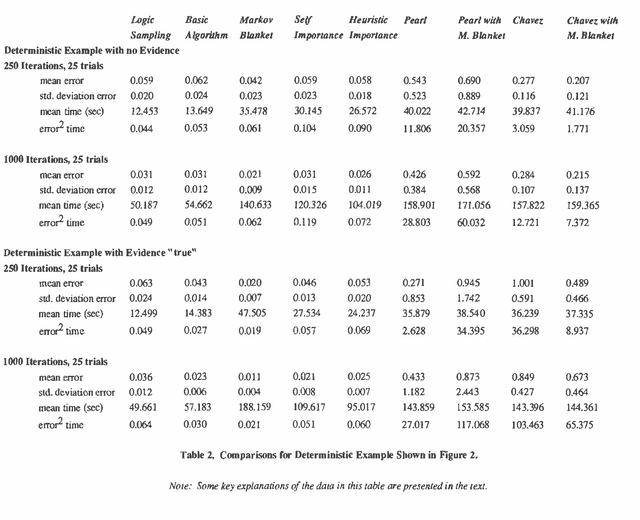
A number of algorithms have been developed to solve probabilistic inference problems on belief networks. These algorithms can be divided into two main groups: exact techniques which exploit the conditional independence revealed when the graph structure is relatively sparse, and probabilistic sampling techniques which exploit the "conductance" of an embedded Markov chain when the conditional probabilities have non-extreme values. In this paper, we investigate a family of "forward" Monte Carlo sampling techniques similar to Logic Sampling [Henrion, 1988] which appear to perform well even in some multiply connected networks with extreme conditional probabilities, and thus would be generally applicable. We consider several enhancements which reduce the posterior variance using this approach and propose a framework and criteria for choosing when to use those enhancements.