Simulation Approaches to General Probabilistic Inference on Belief Networks

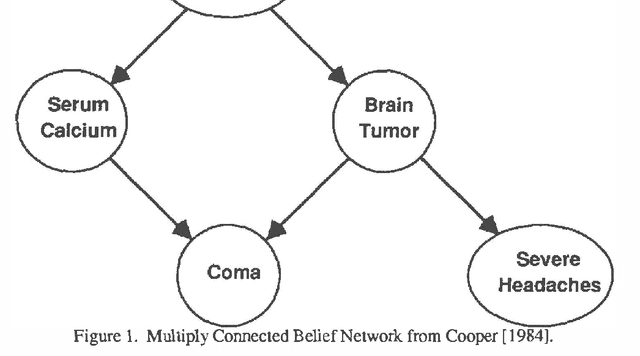
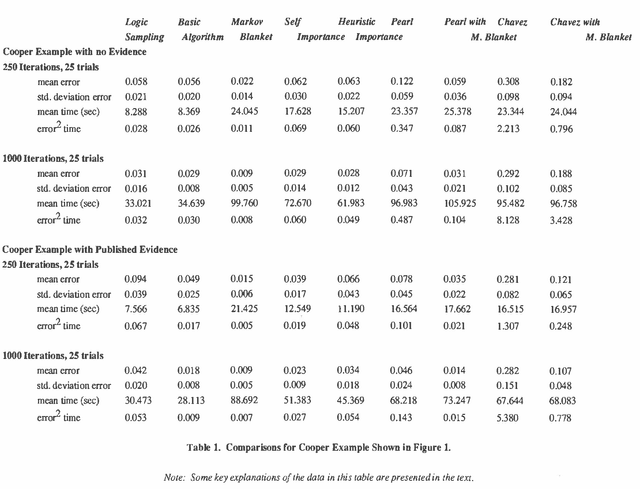
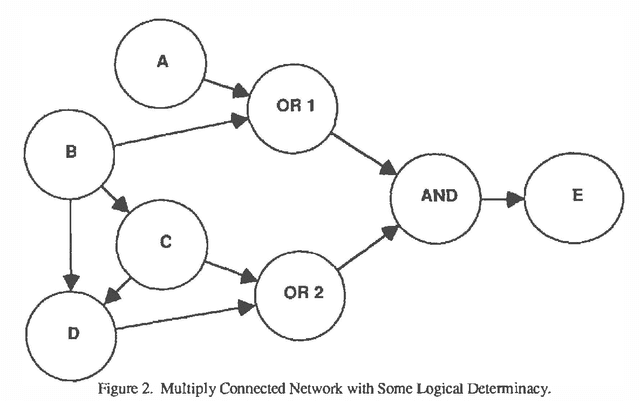
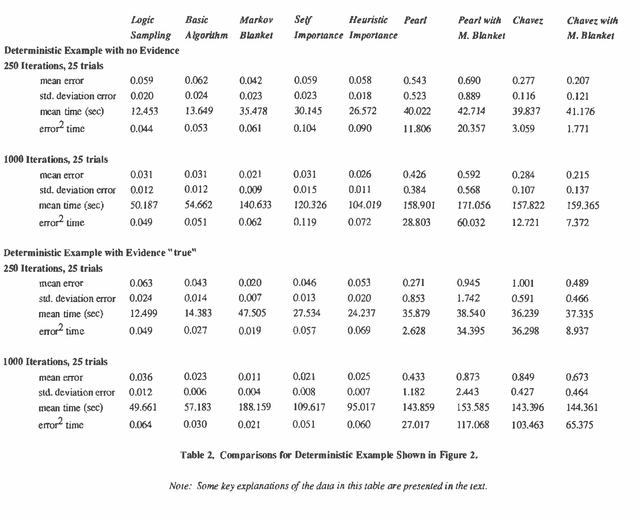
A number of algorithms have been developed to solve probabilistic inference problems on belief networks. These algorithms can be divided into two main groups: exact techniques which exploit the conditional independence revealed when the graph structure is relatively sparse, and probabilistic sampling techniques which exploit the "conductance" of an embedded Markov chain when the conditional probabilities have non-extreme values. In this paper, we investigate a family of "forward" Monte Carlo sampling techniques similar to Logic Sampling [Henrion, 1988] which appear to perform well even in some multiply connected networks with extreme conditional probabilities, and thus would be generally applicable. We consider several enhancements which reduce the posterior variance using this approach and propose a framework and criteria for choosing when to use those enhancements.

Decision Making Using Probabilistic Inference Methods

The analysis of decision making under uncertainty is closely related to the analysis of probabilistic inference. Indeed, much of the research into efficient methods for probabilistic inference in expert systems has been motivated by the fundamental normative arguments of decision theory. In this paper we show how the developments underlying those efficient methods can be applied immediately to decision problems. In addition to general approaches which need know nothing about the actual probabilistic inference method, we suggest some simple modifications to the clustering family of algorithms in order to efficiently incorporate decision making capabilities.

Geometric Implications of the Naive Bayes Assumption

A naive (or Idiot) Bayes network is a network with a single hypothesis node and several observations that are conditionally independent given the hypothesis. We recently surveyed a number of members of the UAI community and discovered a general lack of understanding of the implications of the Naive Bayes assumption on the kinds of problems that can be solved by these networks. It has long been recognized [Minsky 61] that if observations are binary, the decision surfaces in these networks are hyperplanes. We extend this result (hyperplane separability) to Naive Bayes networks with m-ary observations. In addition, we illustrate the effect of observation-observation dependencies on decision surfaces. Finally, we discuss the implications of these results on knowledge acquisition and research in learning.

Learning From What You Don't Observe

The process of diagnosis involves learning about the state of a system from various observations of symptoms or findings about the system. Sophisticated Bayesian (and other) algorithms have been developed to revise and maintain beliefs about the system as observations are made. Nonetheless, diagnostic models have tended to ignore some common sense reasoning exploited by human diagnosticians; In particular, one can learn from which observations have not been made, in the spirit of conversational implicature. There are two concepts that we describe to extract information from the observations not made. First, some symptoms, if present, are more likely to be reported before others. Second, most human diagnosticians and expert systems are economical in their data-gathering, searching first where they are more likely to find symptoms present. Thus, there is a desirable bias toward reporting symptoms that are present. We develop a simple model for these concepts that can significantly improve diagnostic inference.