Simulation Approaches to General Probabilistic Inference on Belief Networks
Paper and Code
Mar 27, 2013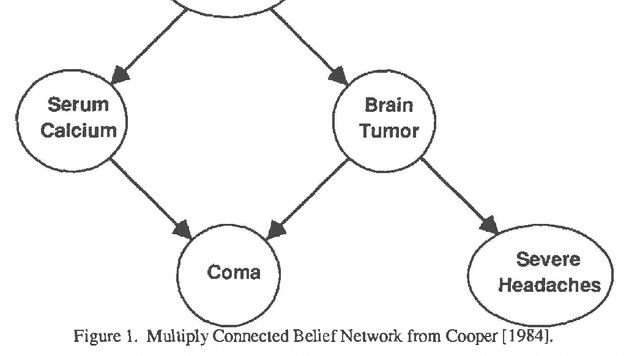
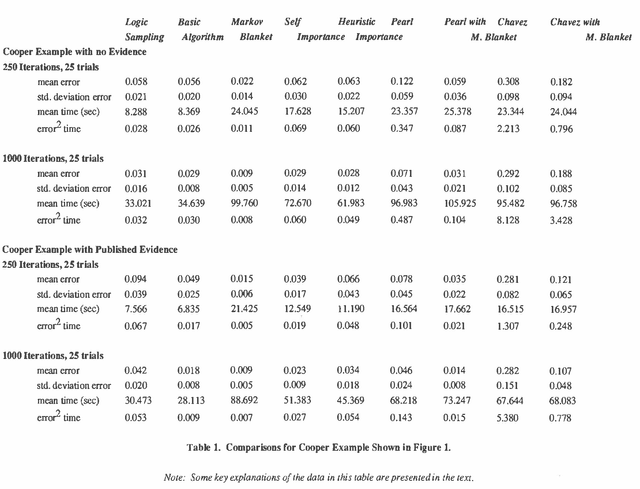
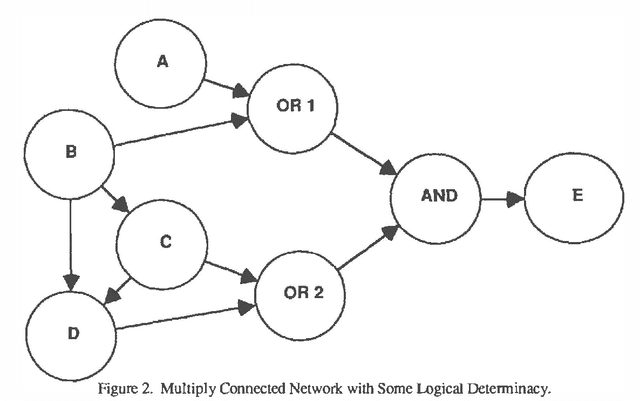
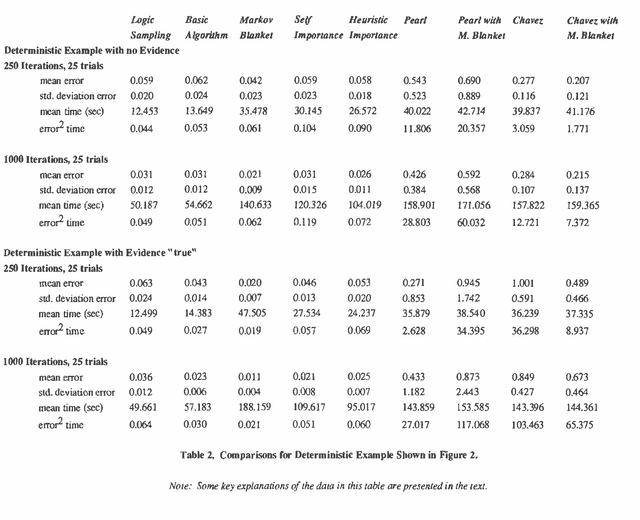
A number of algorithms have been developed to solve probabilistic inference problems on belief networks. These algorithms can be divided into two main groups: exact techniques which exploit the conditional independence revealed when the graph structure is relatively sparse, and probabilistic sampling techniques which exploit the "conductance" of an embedded Markov chain when the conditional probabilities have non-extreme values. In this paper, we investigate a family of "forward" Monte Carlo sampling techniques similar to Logic Sampling [Henrion, 1988] which appear to perform well even in some multiply connected networks with extreme conditional probabilities, and thus would be generally applicable. We consider several enhancements which reduce the posterior variance using this approach and propose a framework and criteria for choosing when to use those enhancements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge