Mixtures of Gaussians and Minimum Relative Entropy Techniques for Modeling Continuous Uncertainties

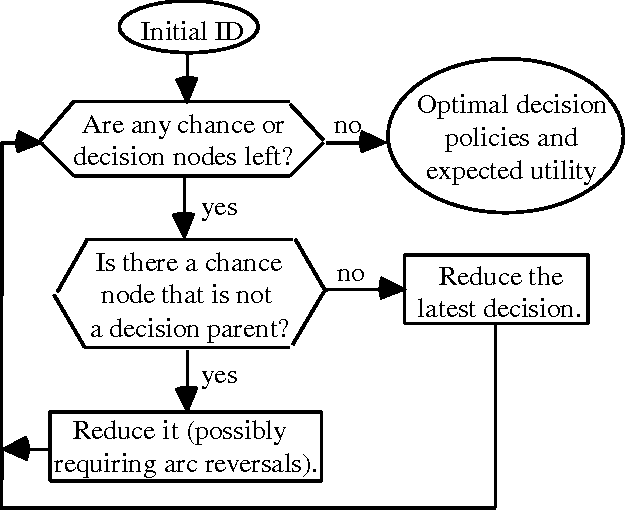
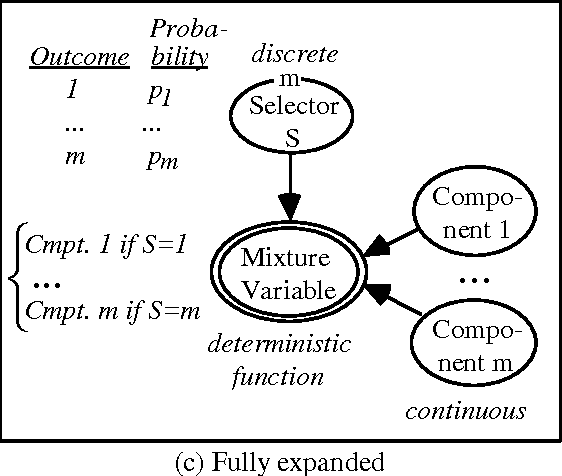
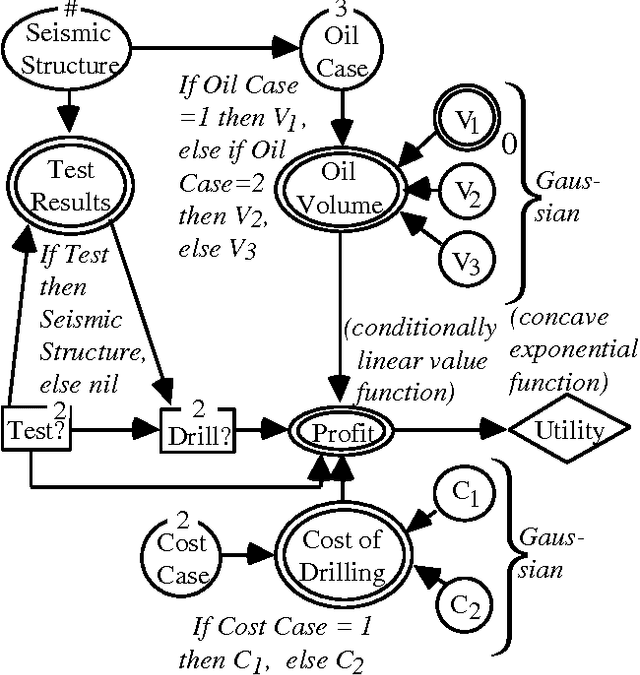
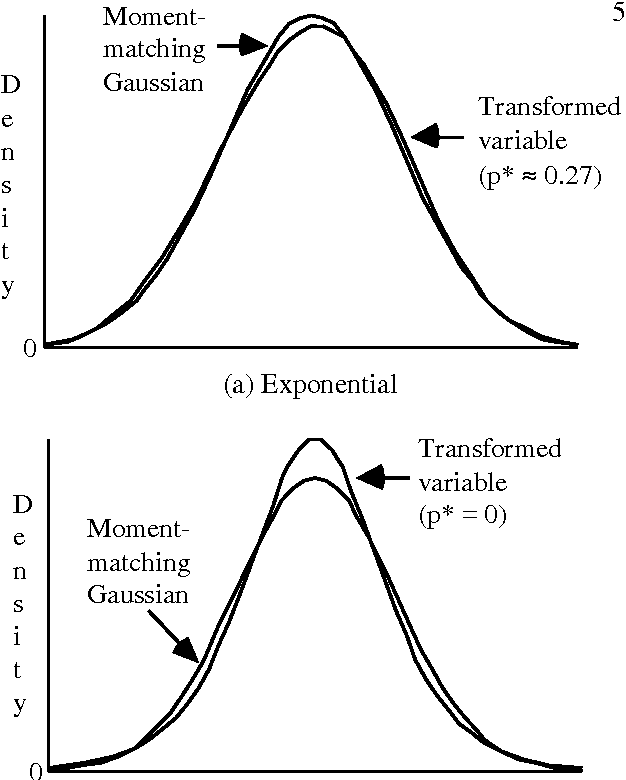
Problems of probabilistic inference and decision making under uncertainty commonly involve continuous random variables. Often these are discretized to a few points, to simplify assessments and computations. An alternative approximation is to fit analytically tractable continuous probability distributions. This approach has potential simplicity and accuracy advantages, especially if variables can be transformed first. This paper shows how a minimum relative entropy criterion can drive both transformation and fitting, illustrating with a power and logarithm family of transformations and mixtures of Gaussian (normal) distributions, which allow use of efficient influence diagram methods. The fitting procedure in this case is the well-known EM algorithm. The selection of the number of components in a fitted mixture distribution is automated with an objective that trades off accuracy and computational cost.