Double Weighted Truncated Nuclear Norm Regularization for Low-Rank Matrix Completion

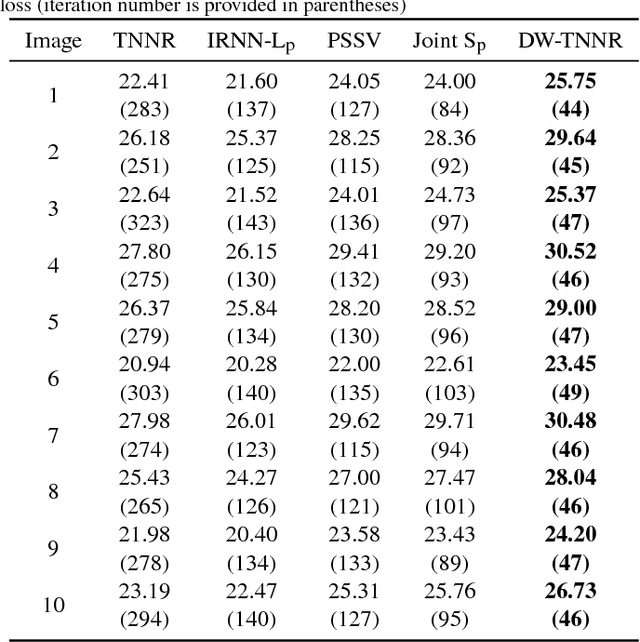
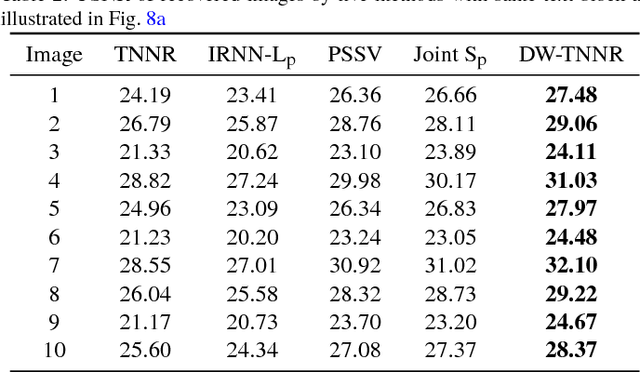
Matrix completion focuses on recovering a matrix from a small subset of its observed elements, and has already gained cumulative attention in computer vision. Many previous approaches formulate this issue as a low-rank matrix approximation problem. Recently, a truncated nuclear norm has been presented as a surrogate of traditional nuclear norm, for better estimation to the rank of a matrix. The truncated nuclear norm regularization (TNNR) method is applicable in real-world scenarios. However, it is sensitive to the selection of the number of truncated singular values and requires numerous iterations to converge. Hereby, this paper proposes a revised approach called the double weighted truncated nuclear norm regularization (DW-TNNR), which assigns different weights to the rows and columns of a matrix separately, to accelerate the convergence with acceptable performance. The DW-TNNR is more robust to the number of truncated singular values than the TNNR. Instead of the iterative updating scheme in the second step of TNNR, this paper devises an efficient strategy that uses a gradient descent manner in a concise form, with a theoretical guarantee in optimization. Sufficient experiments conducted on real visual data prove that DW-TNNR has promising performance and holds the superiority in both speed and accuracy for matrix completion.

Truncated nuclear norm regularization for low-rank tensor completion

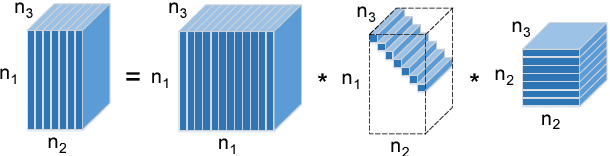
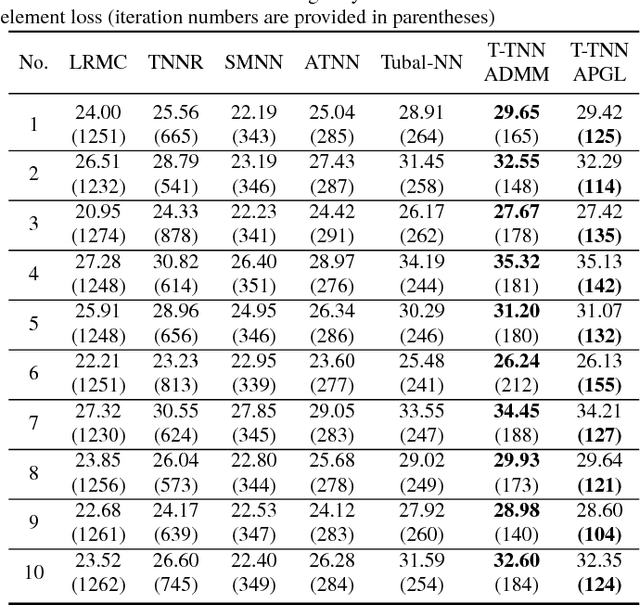
Recently, low-rank tensor completion has become increasingly attractive in recovering incomplete visual data. Considering a color image or video as a three-dimensional (3D) tensor, existing studies have put forward several definitions of tensor nuclear norm. However, they are limited and may not accurately approximate the real rank of a tensor, and they do not explicitly use the low-rank property in optimization. It is proved that the recently proposed truncated nuclear norm (TNN) can replace the traditional nuclear norm, as an improved approximation to the rank of a matrix. In this paper, we propose a new method called the tensor truncated nuclear norm (T-TNN), which suggests a new definition of tensor nuclear norm. The truncated nuclear norm is generalized from the matrix case to the tensor case. With the help of the low rankness of TNN, our approach improves the efficacy of tensor completion. We adopt the definition of the previously proposed tensor singular value decomposition, the alternating direction method of multipliers, and the accelerated proximal gradient line search method in our algorithm. Substantial experiments on real-world videos and images illustrate that the performance of our approach is better than those of previous methods.

Low-Rank Tensor Completion by Truncated Nuclear Norm Regularization

Currently, low-rank tensor completion has gained cumulative attention in recovering incomplete visual data whose partial elements are missing. By taking a color image or video as a three-dimensional (3D) tensor, previous studies have suggested several definitions of tensor nuclear norm. However, they have limitations and may not properly approximate the real rank of a tensor. Besides, they do not explicitly use the low-rank property in optimization. It is proved that the recently proposed truncated nuclear norm (TNN) can replace the traditional nuclear norm, as a better estimation to the rank of a matrix. Thus, this paper presents a new method called the tensor truncated nuclear norm (T-TNN), which proposes a new definition of tensor nuclear norm and extends the truncated nuclear norm from the matrix case to the tensor case. Beneficial from the low rankness of TNN, our approach improves the efficacy of tensor completion. We exploit the previously proposed tensor singular value decomposition and the alternating direction method of multipliers in optimization. Extensive experiments on real-world videos and images demonstrate that the performance of our approach is superior to those of existing methods.