Truncated nuclear norm regularization for low-rank tensor completion
Paper and Code
Jan 07, 2019
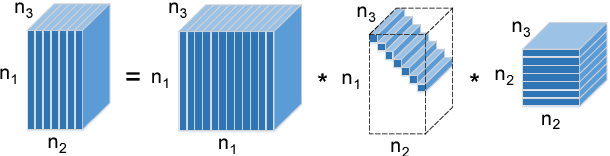

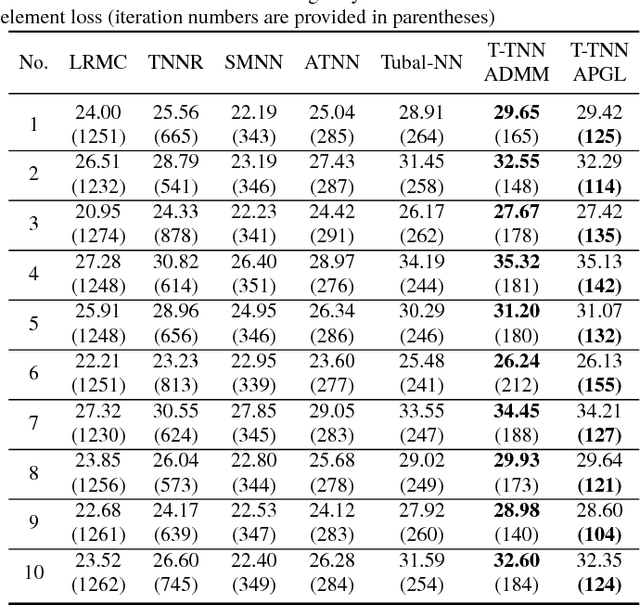
Recently, low-rank tensor completion has become increasingly attractive in recovering incomplete visual data. Considering a color image or video as a three-dimensional (3D) tensor, existing studies have put forward several definitions of tensor nuclear norm. However, they are limited and may not accurately approximate the real rank of a tensor, and they do not explicitly use the low-rank property in optimization. It is proved that the recently proposed truncated nuclear norm (TNN) can replace the traditional nuclear norm, as an improved approximation to the rank of a matrix. In this paper, we propose a new method called the tensor truncated nuclear norm (T-TNN), which suggests a new definition of tensor nuclear norm. The truncated nuclear norm is generalized from the matrix case to the tensor case. With the help of the low rankness of TNN, our approach improves the efficacy of tensor completion. We adopt the definition of the previously proposed tensor singular value decomposition, the alternating direction method of multipliers, and the accelerated proximal gradient line search method in our algorithm. Substantial experiments on real-world videos and images illustrate that the performance of our approach is better than those of previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge