MiniCPM4: Ultra-Efficient LLMs on End Devices

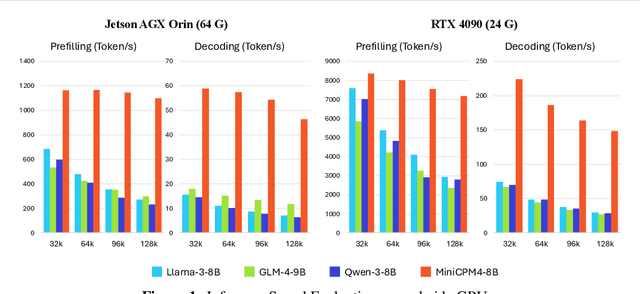
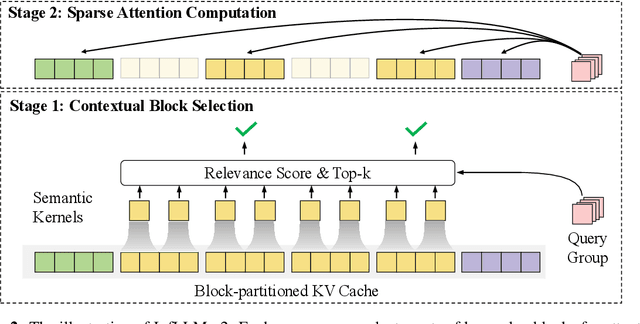
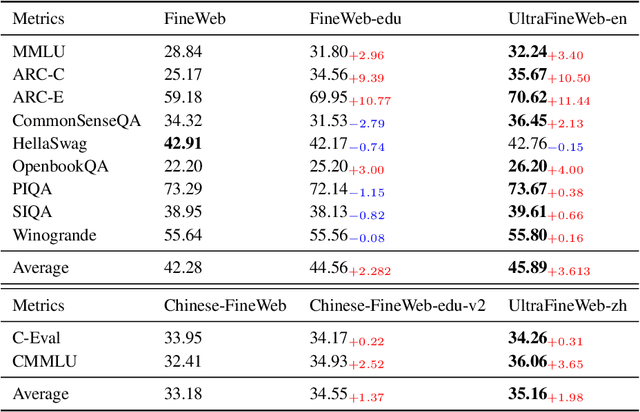
This paper introduces MiniCPM4, a highly efficient large language model (LLM) designed explicitly for end-side devices. We achieve this efficiency through systematic innovation in four key dimensions: model architecture, training data, training algorithms, and inference systems. Specifically, in terms of model architecture, we propose InfLLM v2, a trainable sparse attention mechanism that accelerates both prefilling and decoding phases for long-context processing. Regarding training data, we propose UltraClean, an efficient and accurate pre-training data filtering and generation strategy, and UltraChat v2, a comprehensive supervised fine-tuning dataset. These datasets enable satisfactory model performance to be achieved using just 8 trillion training tokens. Regarding training algorithms, we propose ModelTunnel v2 for efficient pre-training strategy search, and improve existing post-training methods by introducing chunk-wise rollout for load-balanced reinforcement learning and data-efficient tenary LLM, BitCPM. Regarding inference systems, we propose CPM.cu that integrates sparse attention, model quantization, and speculative sampling to achieve efficient prefilling and decoding. To meet diverse on-device requirements, MiniCPM4 is available in two versions, with 0.5B and 8B parameters, respectively. Sufficient evaluation results show that MiniCPM4 outperforms open-source models of similar size across multiple benchmarks, highlighting both its efficiency and effectiveness. Notably, MiniCPM4-8B demonstrates significant speed improvements over Qwen3-8B when processing long sequences. Through further adaptation, MiniCPM4 successfully powers diverse applications, including trustworthy survey generation and tool use with model context protocol, clearly showcasing its broad usability.

ComSearch: Equation Searching with Combinatorial Strategy for Solving Math Word Problems with Weak Supervision

Previous studies have introduced a weakly-supervised paradigm for solving math word problems requiring only the answer value annotation. While these methods search for correct value equation candidates as pseudo labels, they search among a narrow sub-space of the enormous equation space. To address this problem, we propose a novel search algorithm with combinatorial strategy \textbf{ComSearch}, which can compress the search space by excluding mathematically equivalent equations. The compression allows the searching algorithm to enumerate all possible equations and obtain high-quality data. We investigate the noise in the pseudo labels that hold wrong mathematical logic, which we refer to as the \textit{false-matching} problem, and propose a ranking model to denoise the pseudo labels. Our approach holds a flexible framework to utilize two existing supervised math word problem solvers to train pseudo labels, and both achieve state-of-the-art performance in the weak supervision task.

Reverse Operation based Data Augmentation for Solving Math Word Problems

Automatically solving math word problems is a critical task in the field of natural language processing. Recent models have reached their performance bottleneck and require more high-quality data for training. Inspired by human double-checking mechanism, we propose a reverse operation based data augmentation method that makes use of mathematical logic to produce new high-quality math problems and introduce new knowledge points that can give supervision for new mathematical reasoning logic. We apply the augmented data on two SOTA math word problem solving models. Experimental results show the effectiveness of our approach\footnote{We will release our code and data after the paper is accepted.}.