Reinforced Latent Reasoning for LLM-based Recommendation

Large Language Models (LLMs) have demonstrated impressive reasoning capabilities in complex problem-solving tasks, sparking growing interest in their application to preference reasoning in recommendation systems. Existing methods typically rely on fine-tuning with explicit chain-of-thought (CoT) data. However, these methods face significant practical limitations due to (1) the difficulty of obtaining high-quality CoT data in recommendation and (2) the high inference latency caused by generating CoT reasoning. In this work, we explore an alternative approach that shifts from explicit CoT reasoning to compact, information-dense latent reasoning. This approach eliminates the need for explicit CoT generation and improves inference efficiency, as a small set of latent tokens can effectively capture the entire reasoning process. Building on this idea, we propose $\textit{\underline{R}einforced \underline{Latent} \underline{R}easoning for \underline{R}ecommendation}$ (LatentR$^3$), a novel end-to-end training framework that leverages reinforcement learning (RL) to optimize latent reasoning without relying on any CoT data.LatentR$^3$ adopts a two-stage training strategy: first, supervised fine-tuning to initialize the latent reasoning module, followed by pure RL training to encourage exploration through a rule-based reward design. Our RL implementation is based on a modified GRPO algorithm, which reduces computational overhead during training and introduces continuous reward signals for more efficient learning. Extensive experiments demonstrate that LatentR$^3$ enables effective latent reasoning without any direct supervision of the reasoning process, significantly improving performance when integrated with different LLM-based recommendation methods. Our codes are available at https://anonymous.4open.science/r/R3-A278/.

Learning Subjective Time-Series Data via Utopia Label Distribution Approximation

Subjective time-series regression (STR) tasks have gained increasing attention recently. However, most existing methods overlook the label distribution bias in STR data, which results in biased models. Emerging studies on imbalanced regression tasks, such as age estimation and depth estimation, hypothesize that the prior label distribution of the dataset is uniform. However, we observe that the label distributions of training and test sets in STR tasks are likely to be neither uniform nor identical. This distinct feature calls for new approaches that estimate more reasonable distributions to train a fair model. In this work, we propose Utopia Label Distribution Approximation (ULDA) for time-series data, which makes the training label distribution closer to real-world but unknown (utopia) label distribution. This would enhance the model's fairness. Specifically, ULDA first convolves the training label distribution by a Gaussian kernel. After convolution, the required sample quantity at each regression label may change. We further devise the Time-slice Normal Sampling (TNS) to generate new samples when the required sample quantity is greater than the initial sample quantity, and the Convolutional Weighted Loss (CWL) to lower the sample weight when the required sample quantity is less than the initial quantity. These two modules not only assist the model training on the approximated utopia label distribution, but also maintain the sample continuity in temporal context space. To the best of our knowledge, ULDA is the first method to address the label distribution bias in time-series data. Extensive experiments demonstrate that ULDA lifts the state-of-the-art performance on two STR tasks and three benchmark datasets.

Gaussian-smoothed Imbalance Data Improves Speech Emotion Recognition

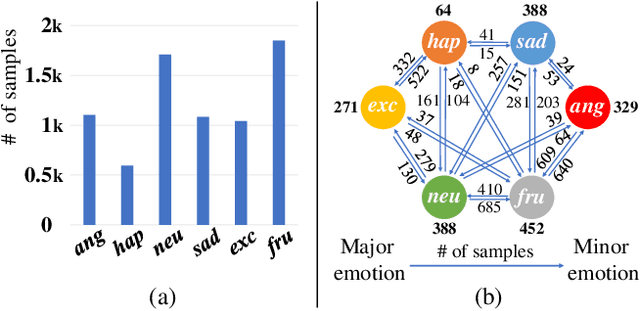
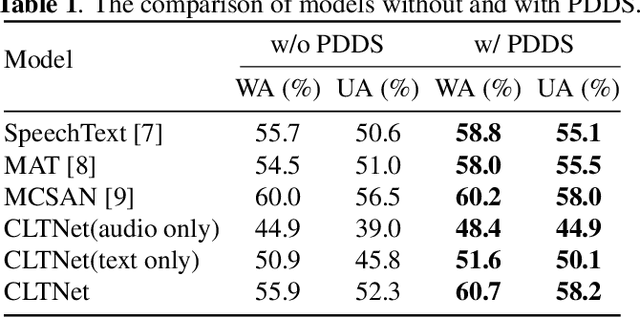
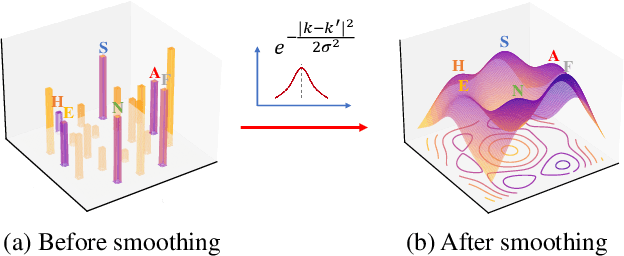
In speech emotion recognition tasks, models learn emotional representations from datasets. We find the data distribution in the IEMOCAP dataset is very imbalanced, which may harm models to learn a better representation. To address this issue, we propose a novel Pairwise-emotion Data Distribution Smoothing (PDDS) method. PDDS considers that the distribution of emotional data should be smooth in reality, then applies Gaussian smoothing to emotion-pairs for constructing a new training set with a smoother distribution. The required new data are complemented using the mixup augmentation. As PDDS is model and modality agnostic, it is evaluated with three SOTA models on the IEMOCAP dataset. The experimental results show that these models are improved by 0.2\% - 4.8\% and 1.5\% - 5.9\% in terms of WA and UA. In addition, an ablation study demonstrates that the key advantage of PDDS is the reasonable data distribution rather than a simple data augmentation.