Adaptively Point-weighting Curriculum Learning

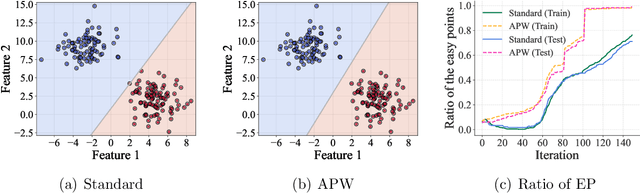
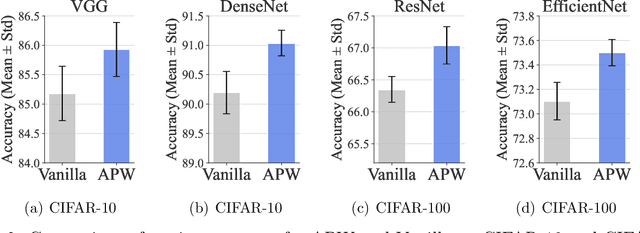
Curriculum learning (CL) is referred to as a training strategy that makes easy samples learned first and then fits hard samples. It imitates the process of humans learning knowledge, and has become a potential manner of effectively training deep networks. In this study, we develop the adaptively point-weighting (APW) curriculum learning algorithm, which adaptively assigns the weight to every training sample not only based on its training error but also considering the current training state of the network. Specifically, in the early training phase, it increases the weights of easy samples to make the network rapidly capture the overall characteristics of the dataset; and in the later training phase, the weights of hard points rise to improve the fitting performance on the discrete local regions. Moreover, we also present the theoretical analysis on the properties of APW including training effectiveness, training feasibility, training stability, and generalization performance. The numerical experiments support the superiority of APW and demonstrate the validity of our theoretical findings.

Understanding Deep Neural Networks via Linear Separability of Hidden Layers

In this paper, we measure the linear separability of hidden layer outputs to study the characteristics of deep neural networks. In particular, we first propose Minkowski difference based linear separability measures (MD-LSMs) to evaluate the linear separability degree of two points sets. Then, we demonstrate that there is a synchronicity between the linear separability degree of hidden layer outputs and the network training performance, i.e., if the updated weights can enhance the linear separability degree of hidden layer outputs, the updated network will achieve a better training performance, and vice versa. Moreover, we study the effect of activation function and network size (including width and depth) on the linear separability of hidden layers. Finally, we conduct the numerical experiments to validate our findings on some popular deep networks including multilayer perceptron (MLP), convolutional neural network (CNN), deep belief network (DBN), ResNet, VGGNet, AlexNet, vision transformer (ViT) and GoogLeNet.

Revisiting PINNs: Generative Adversarial Physics-informed Neural Networks and Point-weighting Method

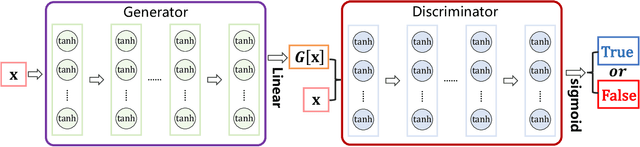
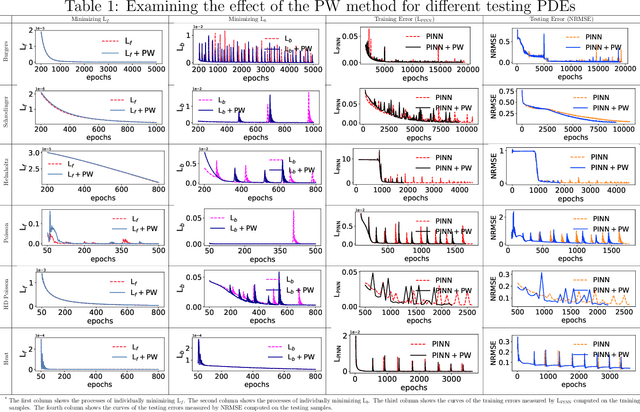
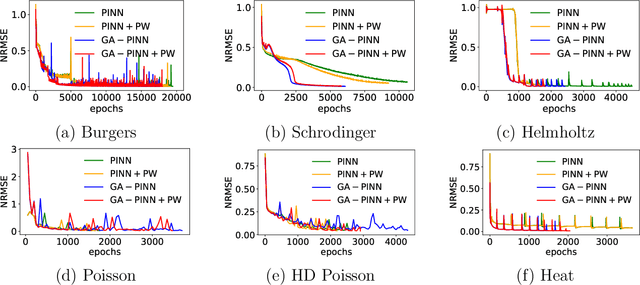
Physics-informed neural networks (PINNs) provide a deep learning framework for numerically solving partial differential equations (PDEs), and have been widely used in a variety of PDE problems. However, there still remain some challenges in the application of PINNs: 1) the mechanism of PINNs is unsuitable (at least cannot be directly applied) to exploiting a small size of (usually very few) extra informative samples to refine the networks; and 2) the efficiency of training PINNs often becomes low for some complicated PDEs. In this paper, we propose the generative adversarial physics-informed neural network (GA-PINN), which integrates the generative adversarial (GA) mechanism with the structure of PINNs, to improve the performance of PINNs by exploiting only a small size of exact solutions to the PDEs. Inspired from the weighting strategy of the Adaboost method, we then introduce a point-weighting (PW) method to improve the training efficiency of PINNs, where the weight of each sample point is adaptively updated at each training iteration. The numerical experiments show that GA-PINNs outperform PINNs in many well-known PDEs and the PW method also improves the efficiency of training PINNs and GA-PINNs.