Wenjun Cai
Partitioned Active Learning for Heterogeneous Systems
May 14, 2021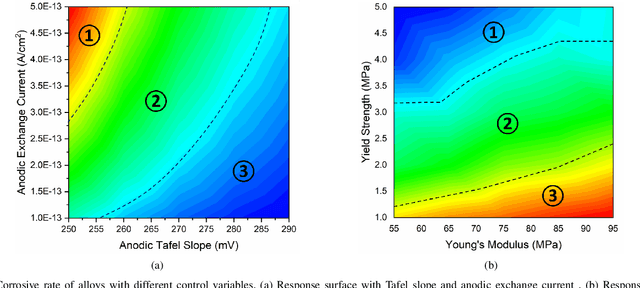
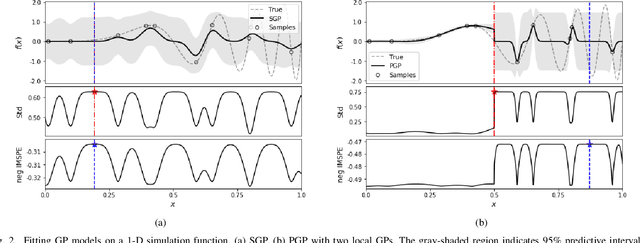
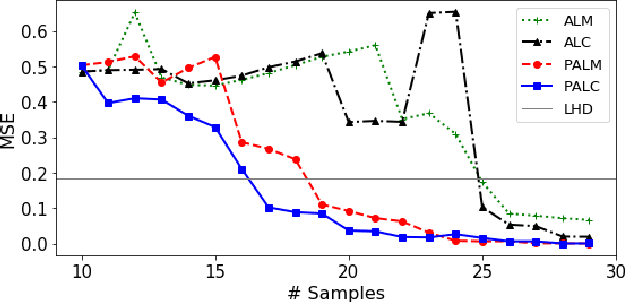
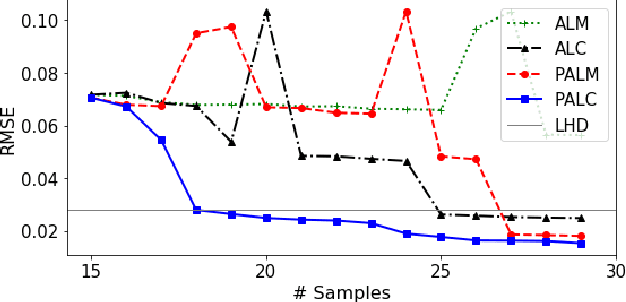
Abstract:Cost-effective and high-precision surrogate modeling is a cornerstone of automated industrial and engineering systems. Active learning coupled with Gaussian process (GP) surrogate modeling is an indispensable tool for demanding and complex systems, while the existence of heterogeneity in underlying systems may adversely affect the modeling process. In order to improve the learning efficiency under the regime, we propose the partitioned active learning strategy established upon partitioned GP (PGP) modeling. Our strategy seeks the most informative design point for PGP modeling systematically in twosteps. The global searching scheme accelerates the exploration aspect of active learning by investigating the most uncertain design space, and the local searching exploits the active learning criterion induced by the local GP model. We also provide numerical remedies to alleviate the computational cost of active learning, thereby allowing the proposed method to incorporate a large amount of candidates. The proposed method is applied to numerical simulation and real world cases endowed with heterogeneities in which surrogate models are constructed to embed in (i) the cost-efficient automatic fuselage shape control system; and (ii) the optimal design system of tribocorrosion-resistant alloys. The results show that our approach outperforms benchmark methods.
NP-ODE: Neural Process Aided Ordinary Differential Equations for Uncertainty Quantification of Finite Element Analysis
Dec 12, 2020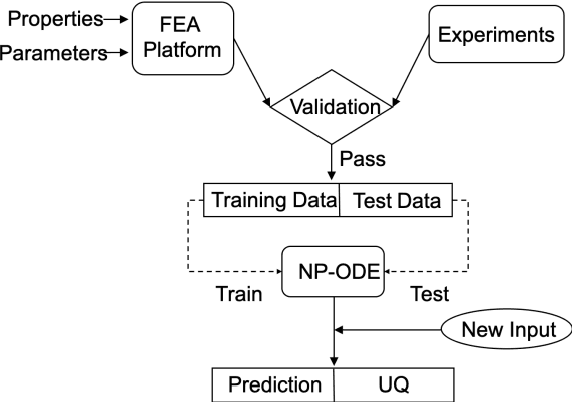
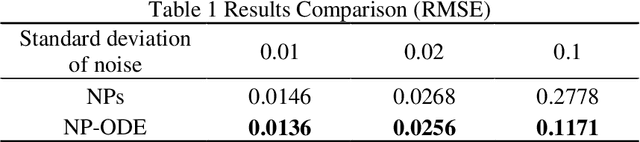
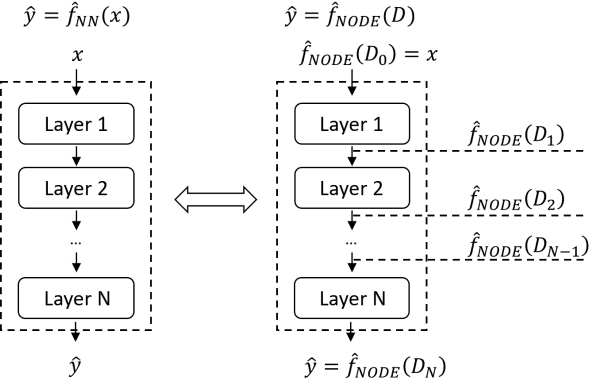
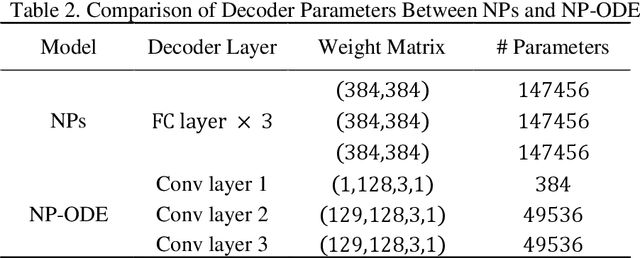
Abstract:Finite element analysis (FEA) has been widely used to generate simulations of complex and nonlinear systems. Despite its strength and accuracy, the limitations of FEA can be summarized into two aspects: a) running high-fidelity FEA often requires significant computational cost and consumes a large amount of time; b) FEA is a deterministic method that is insufficient for uncertainty quantification (UQ) when modeling complex systems with various types of uncertainties. In this paper, a physics-informed data-driven surrogate model, named Neural Process Aided Ordinary Differential Equation (NP-ODE), is proposed to model the FEA simulations and capture both input and output uncertainties. To validate the advantages of the proposed NP-ODE, we conduct experiments on both the simulation data generated from a given ordinary differential equation and the data collected from a real FEA platform for tribocorrosion. The performances of the proposed NP-ODE and several benchmark methods are compared. The results show that the proposed NP-ODE outperforms benchmark methods. The NP-ODE method realizes the smallest predictive error as well as generates the most reasonable confidence interval having the best coverage on testing data points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge