Adaptive Split Balancing for Optimal Random Forest

While random forests are commonly used for regression problems, existing methods often lack adaptability in complex situations or lose optimality under simple, smooth scenarios. In this study, we introduce the adaptive split balancing forest (ASBF), capable of learning tree representations from data while simultaneously achieving minimax optimality under the Lipschitz class. To exploit higher-order smoothness levels, we further propose a localized version that attains the minimax rate under the H\"older class $\mathcal{H}^{q,\beta}$ for any $q\in\mathbb{N}$ and $\beta\in(0,1]$. Rather than relying on the widely-used random feature selection, we consider a balanced modification to existing approaches. Our results indicate that an over-reliance on auxiliary randomness may compromise the approximation power of tree models, leading to suboptimal results. Conversely, a less random, more balanced approach demonstrates optimality. Additionally, we establish uniform upper bounds and explore the application of random forests in average treatment effect estimation problems. Through simulation studies and real-data applications, we demonstrate the superior empirical performance of the proposed methods over existing random forests.

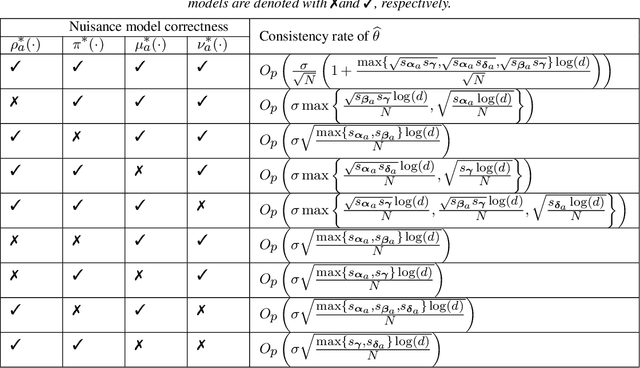
Dynamic treatment effects: high-dimensional inference under model misspecification

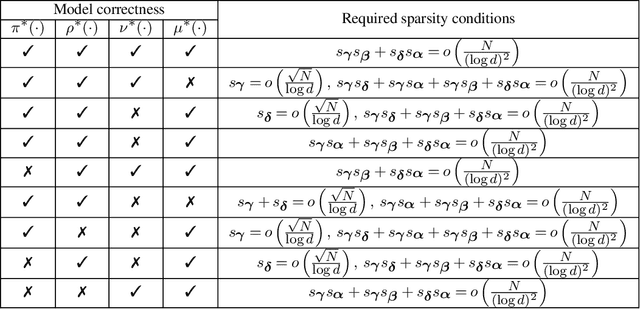
This paper considers the inference for heterogeneous treatment effects in dynamic settings that covariates and treatments are longitudinal. We focus on high-dimensional cases that the sample size, $N$, is potentially much larger than the covariate vector's dimension, $d$. The marginal structural mean models are considered. We propose a "sequential model doubly robust" estimator constructed based on "moment targeted" nuisance estimators. Such nuisance estimators are carefully designed through non-standard loss functions, reducing the bias resulting from potential model misspecifications. We achieve $\sqrt N$-inference even when model misspecification occurs. We only require one nuisance model to be correctly specified at each time spot. Such model correctness conditions are weaker than all the existing work, even containing the literature on low dimensions.

High-dimensional Inference for Dynamic Treatment Effects

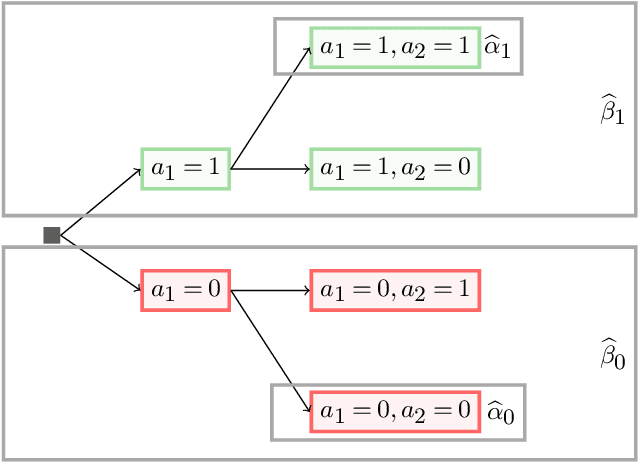
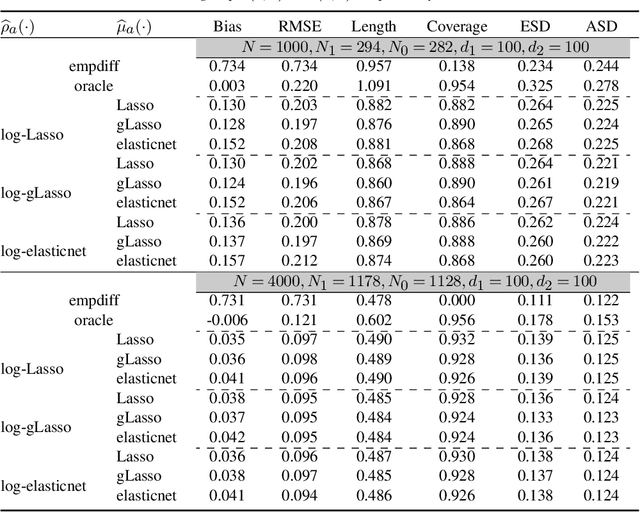
This paper proposes a confidence interval construction for heterogeneous treatment effects in the context of multi-stage experiments with $N$ samples and high-dimensional, $d$, confounders. Our focus is on the case of $d\gg N$, but the results obtained also apply to low-dimensional cases. We showcase that the bias of regularized estimation, unavoidable in high-dimensional covariate spaces, is mitigated with a simple double-robust score. In this way, no additional bias removal is necessary, and we obtain root-$N$ inference results while allowing multi-stage interdependency of the treatments and covariates. Memoryless property is also not assumed; treatment can possibly depend on all previous treatment assignments and all previous multi-stage confounders. Our results rely on certain sparsity assumptions of the underlying dependencies. We discover new product rate conditions necessary for robust inference with dynamic treatments.