Adaptive Split Balancing for Optimal Random Forest
Paper and Code
Feb 17, 2024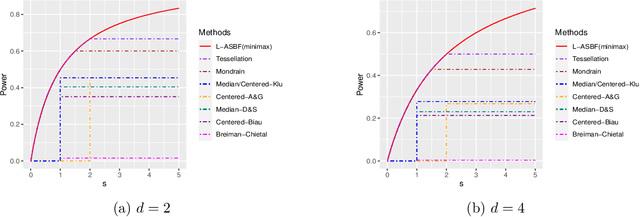
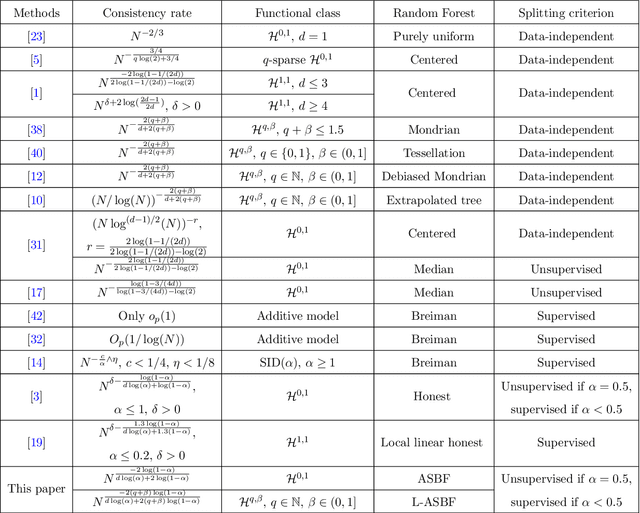
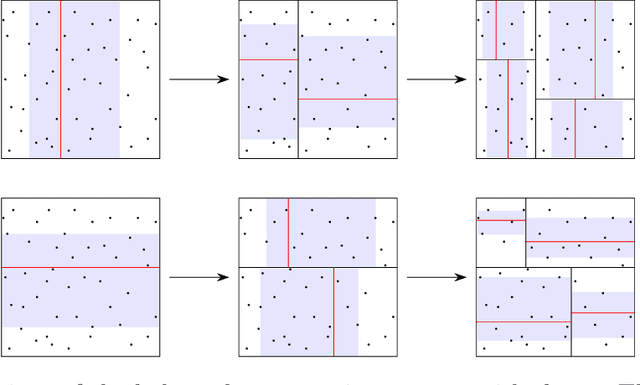
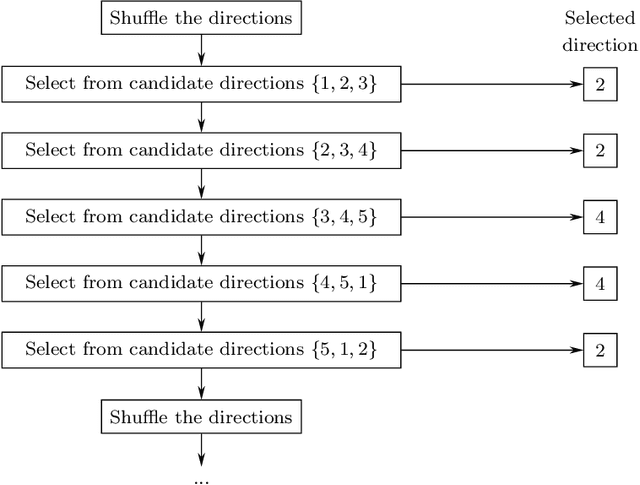
While random forests are commonly used for regression problems, existing methods often lack adaptability in complex situations or lose optimality under simple, smooth scenarios. In this study, we introduce the adaptive split balancing forest (ASBF), capable of learning tree representations from data while simultaneously achieving minimax optimality under the Lipschitz class. To exploit higher-order smoothness levels, we further propose a localized version that attains the minimax rate under the H\"older class $\mathcal{H}^{q,\beta}$ for any $q\in\mathbb{N}$ and $\beta\in(0,1]$. Rather than relying on the widely-used random feature selection, we consider a balanced modification to existing approaches. Our results indicate that an over-reliance on auxiliary randomness may compromise the approximation power of tree models, leading to suboptimal results. Conversely, a less random, more balanced approach demonstrates optimality. Additionally, we establish uniform upper bounds and explore the application of random forests in average treatment effect estimation problems. Through simulation studies and real-data applications, we demonstrate the superior empirical performance of the proposed methods over existing random forests.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge