Weijia Shao
Stylized Synthetic Augmentation further improves Corruption Robustness
Dec 19, 2025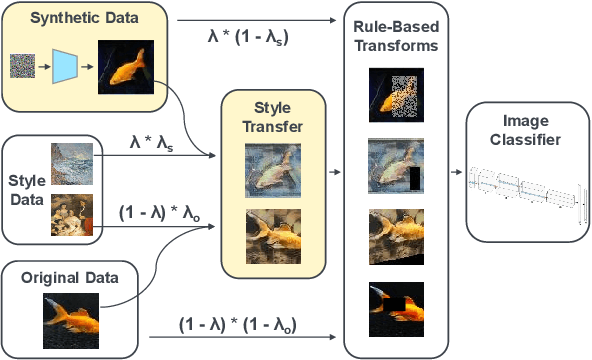

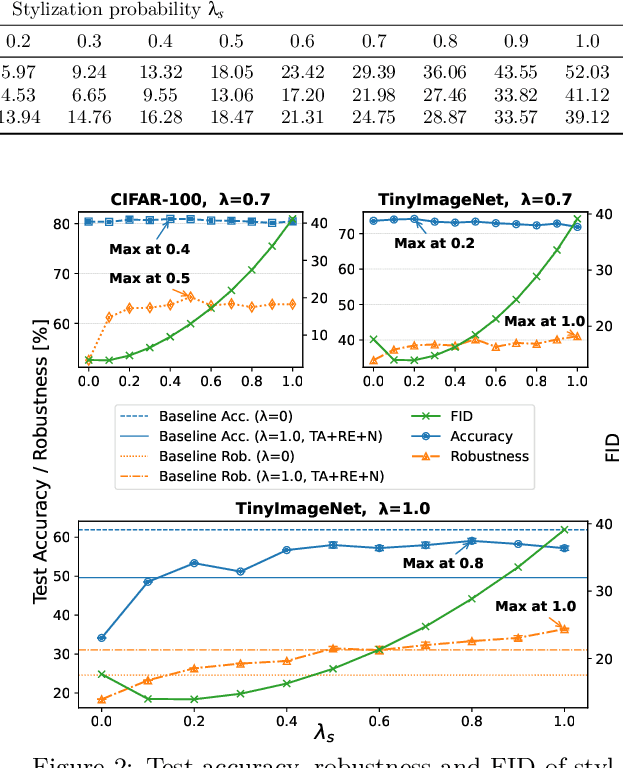
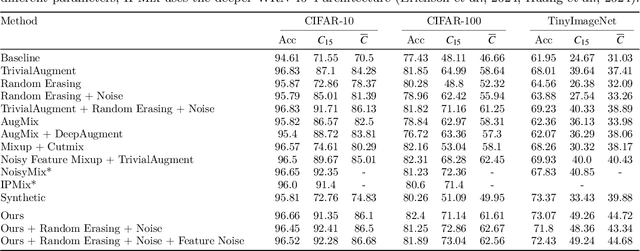
Abstract:This paper proposes a training data augmentation pipeline that combines synthetic image data with neural style transfer in order to address the vulnerability of deep vision models to common corruptions. We show that although applying style transfer on synthetic images degrades their quality with respect to the common Frechet Inception Distance (FID) metric, these images are surprisingly beneficial for model training. We conduct a systematic empirical analysis of the effects of both augmentations and their key hyperparameters on the performance of image classifiers. Our results demonstrate that stylization and synthetic data complement each other well and can be combined with popular rule-based data augmentation techniques such as TrivialAugment, while not working with others. Our method achieves state-of-the-art corruption robustness on several small-scale image classification benchmarks, reaching 93.54%, 74.9% and 50.86% robust accuracy on CIFAR-10-C, CIFAR-100-C and TinyImageNet-C, respectively
Structured Universal Adversarial Attacks on Object Detection for Video Sequences
Oct 16, 2025Abstract:Video-based object detection plays a vital role in safety-critical applications. While deep learning-based object detectors have achieved impressive performance, they remain vulnerable to adversarial attacks, particularly those involving universal perturbations. In this work, we propose a minimally distorted universal adversarial attack tailored for video object detection, which leverages nuclear norm regularization to promote structured perturbations concentrated in the background. To optimize this formulation efficiently, we employ an adaptive, optimistic exponentiated gradient method that enhances both scalability and convergence. Our results demonstrate that the proposed attack outperforms both low-rank projected gradient descent and Frank-Wolfe based attacks in effectiveness while maintaining high stealthiness. All code and data are publicly available at https://github.com/jsve96/AO-Exp-Attack.
Combined Image Data Augmentations diminish the benefits of Adaptive Label Smoothing
Jul 22, 2025Abstract:Soft augmentation regularizes the supervised learning process of image classifiers by reducing label confidence of a training sample based on the magnitude of random-crop augmentation applied to it. This paper extends this adaptive label smoothing framework to other types of aggressive augmentations beyond random-crop. Specifically, we demonstrate the effectiveness of the method for random erasing and noise injection data augmentation. Adaptive label smoothing permits stronger regularization via higher-intensity Random Erasing. However, its benefits vanish when applied with a diverse range of image transformations as in the state-of-the-art TrivialAugment method, and excessive label smoothing harms robustness to common corruptions. Our findings suggest that adaptive label smoothing should only be applied when the training data distribution is dominated by a limited, homogeneous set of image transformation types.
Adaptive Stochastic Optimisation of Nonconvex Composite Objectives
Nov 21, 2022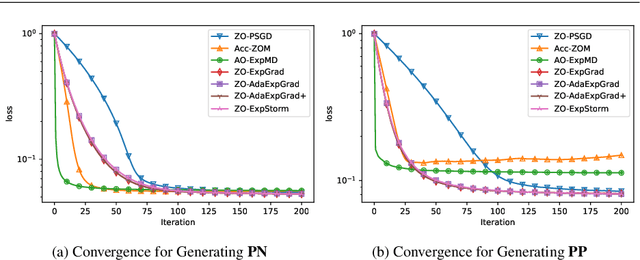
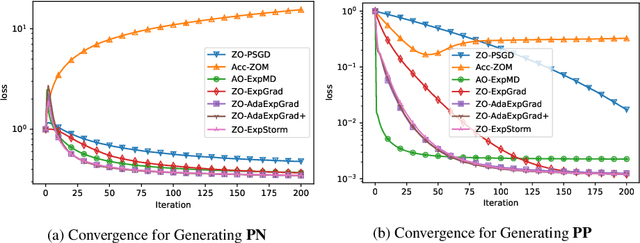
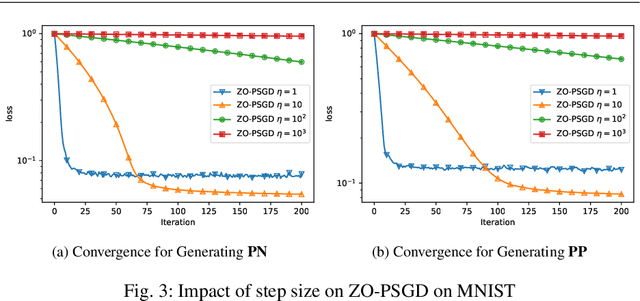
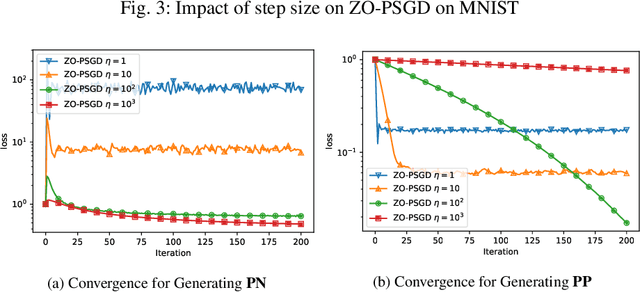
Abstract:In this paper, we propose and analyse a family of generalised stochastic composite mirror descent algorithms. With adaptive step sizes, the proposed algorithms converge without requiring prior knowledge of the problem. Combined with an entropy-like update-generating function, these algorithms perform gradient descent in the space equipped with the maximum norm, which allows us to exploit the low-dimensional structure of the decision sets for high-dimensional problems. Together with a sampling method based on the Rademacher distribution and variance reduction techniques, the proposed algorithms guarantee a logarithmic complexity dependence on dimensionality for zeroth-order optimisation problems.
Adaptive Zeroth-Order Optimisation of Nonconvex Composite Objectives
Aug 14, 2022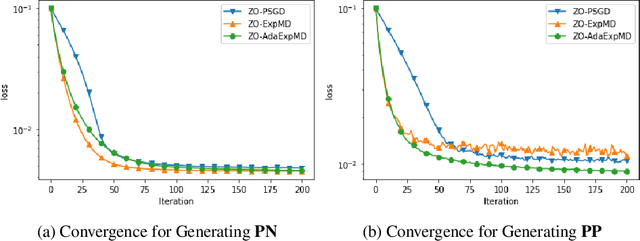
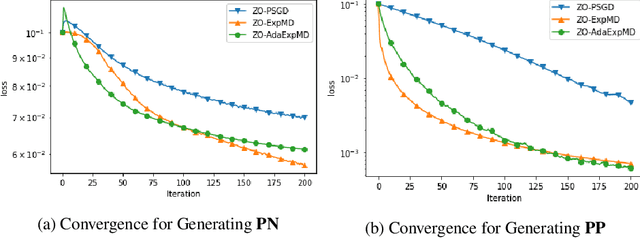
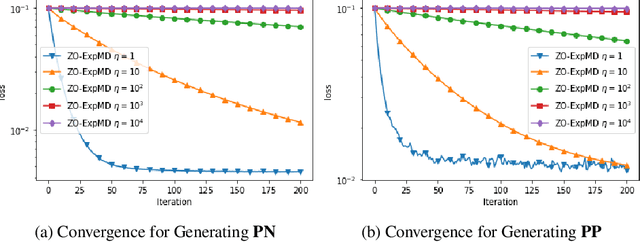
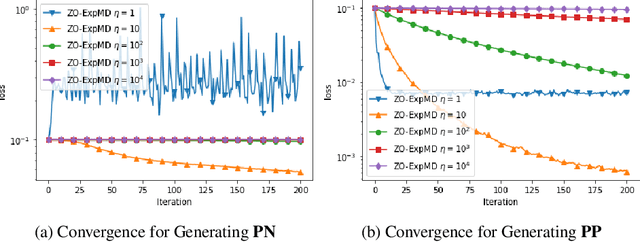
Abstract:In this paper, we propose and analyze algorithms for zeroth-order optimization of non-convex composite objectives, focusing on reducing the complexity dependence on dimensionality. This is achieved by exploiting the low dimensional structure of the decision set using the stochastic mirror descent method with an entropy alike function, which performs gradient descent in the space equipped with the maximum norm. To improve the gradient estimation, we replace the classic Gaussian smoothing method with a sampling method based on the Rademacher distribution and show that the mini-batch method copes with the non-Euclidean geometry. To avoid tuning hyperparameters, we analyze the adaptive stepsizes for the general stochastic mirror descent and show that the adaptive version of the proposed algorithm converges without requiring prior knowledge about the problem.
Optimistic Optimisation of Composite Objective with Exponentiated Update
Aug 08, 2022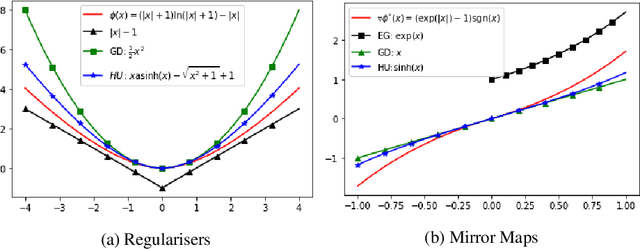
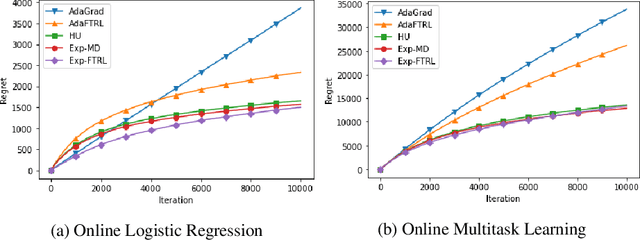
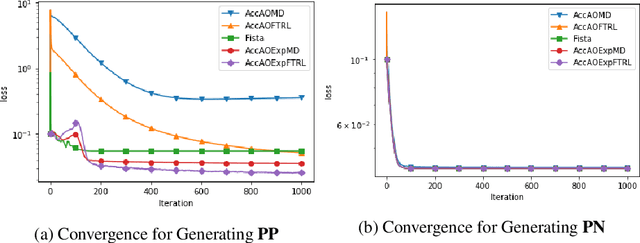
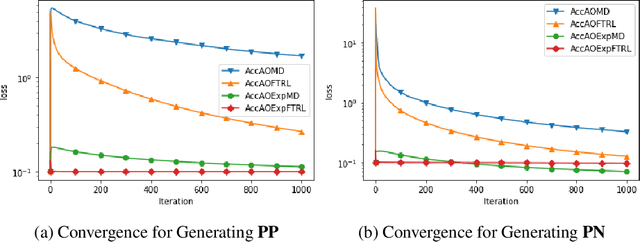
Abstract:This paper proposes a new family of algorithms for the online optimisation of composite objectives. The algorithms can be interpreted as the combination of the exponentiated gradient and $p$-norm algorithm. Combined with algorithmic ideas of adaptivity and optimism, the proposed algorithms achieve a sequence-dependent regret upper bound, matching the best-known bounds for sparse target decision variables. Furthermore, the algorithms have efficient implementations for popular composite objectives and constraints and can be converted to stochastic optimisation algorithms with the optimal accelerated rate for smooth objectives.
Graduated Optimization of Black-Box Functions
Jun 04, 2019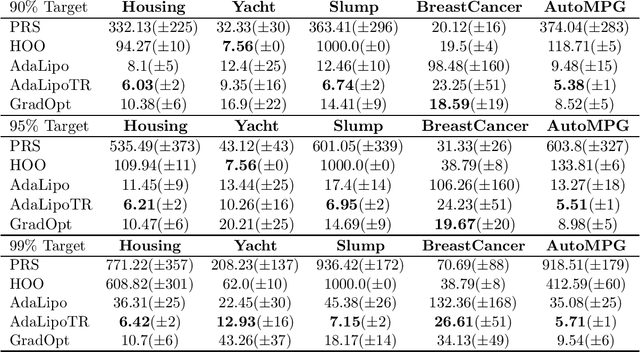
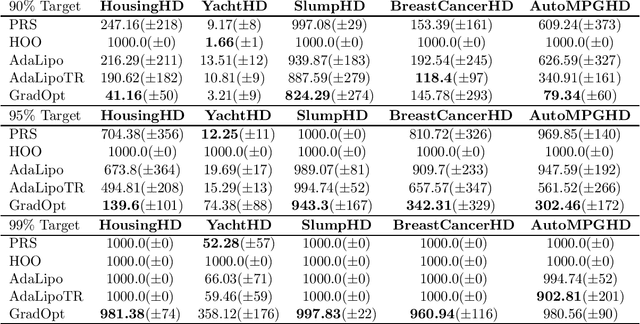
Abstract:Motivated by the problem of tuning hyperparameters in machine learning, we present a new approach for gradually and adaptively optimizing an unknown function using estimated gradients. We validate the empirical performance of the proposed idea on both low and high dimensional problems. The experimental results demonstrate the advantages of our approach for tuning high dimensional hyperparameters in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge