Adaptive Stochastic Optimisation of Nonconvex Composite Objectives
Paper and Code
Nov 21, 2022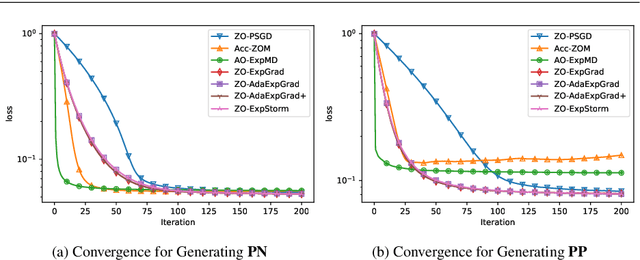
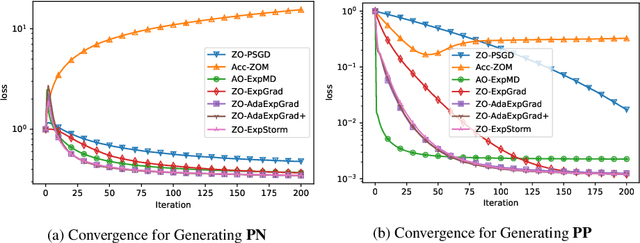
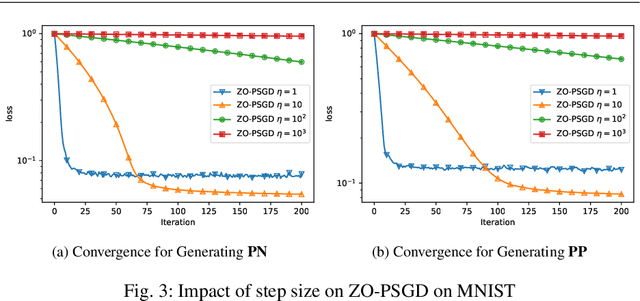
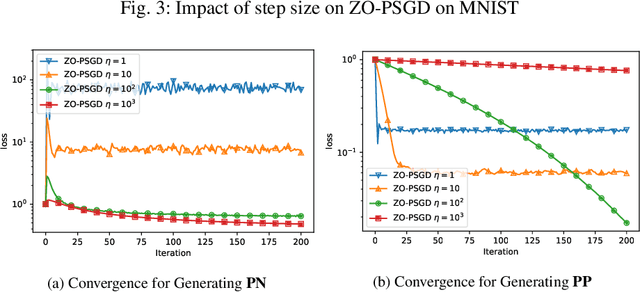
In this paper, we propose and analyse a family of generalised stochastic composite mirror descent algorithms. With adaptive step sizes, the proposed algorithms converge without requiring prior knowledge of the problem. Combined with an entropy-like update-generating function, these algorithms perform gradient descent in the space equipped with the maximum norm, which allows us to exploit the low-dimensional structure of the decision sets for high-dimensional problems. Together with a sampling method based on the Rademacher distribution and variance reduction techniques, the proposed algorithms guarantee a logarithmic complexity dependence on dimensionality for zeroth-order optimisation problems.
* arXiv admin note: substantial text overlap with arXiv:2208.04579
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge