StressNet: Deep Learning to Predict Stress With Fracture Propagation in Brittle Materials

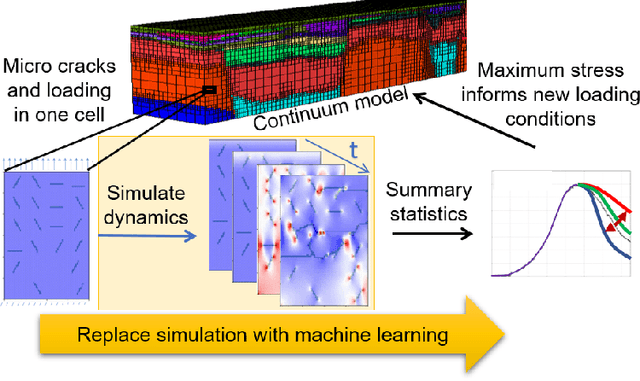
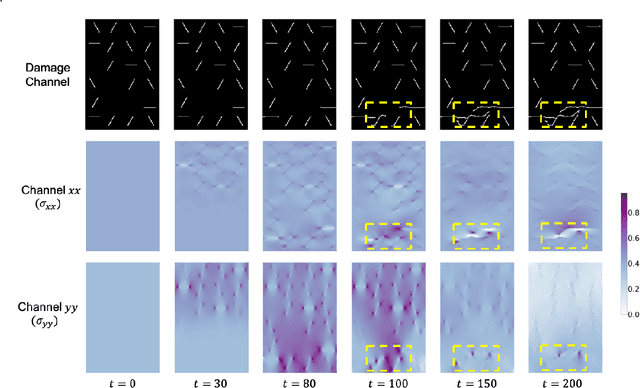
Catastrophic failure in brittle materials is often due to the rapid growth and coalescence of cracks aided by high internal stresses. Hence, accurate prediction of maximum internal stress is critical to predicting time to failure and improving the fracture resistance and reliability of materials. Existing high-fidelity methods, such as the Finite-Discrete Element Model (FDEM), are limited by their high computational cost. Therefore, to reduce computational cost while preserving accuracy, a novel deep learning model, "StressNet," is proposed to predict the entire sequence of maximum internal stress based on fracture propagation and the initial stress data. More specifically, the Temporal Independent Convolutional Neural Network (TI-CNN) is designed to capture the spatial features of fractures like fracture path and spall regions, and the Bidirectional Long Short-term Memory (Bi-LSTM) Network is adapted to capture the temporal features. By fusing these features, the evolution in time of the maximum internal stress can be accurately predicted. Moreover, an adaptive loss function is designed by dynamically integrating the Mean Squared Error (MSE) and the Mean Absolute Percentage Error (MAPE), to reflect the fluctuations in maximum internal stress. After training, the proposed model is able to compute accurate multi-step predictions of maximum internal stress in approximately 20 seconds, as compared to the FDEM run time of 4 hours, with an average MAPE of 2% relative to test data.

CPAC-Conv: CP-decomposition to Approximately Compress Convolutional Layers in Deep Learning

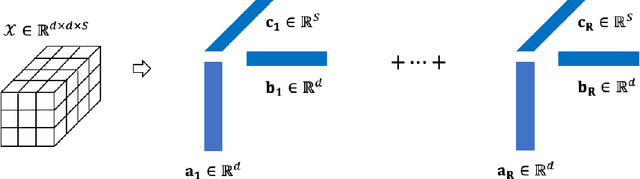
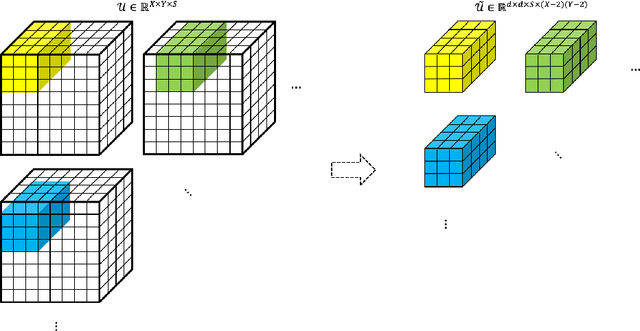
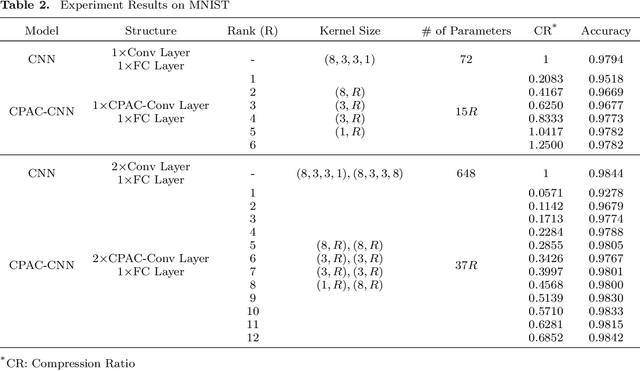
Feature extraction for tensor data serves as an important step in many tasks such as anomaly detection, process monitoring, image classification, and quality control. Although many methods have been proposed for tensor feature extraction, there are still two challenges that need to be addressed: 1) how to reduce the computation cost for high dimensional and large volume tensor data; 2) how to interpret the output features and evaluate their significance. Although the most recent methods in deep learning, such as Convolutional Neural Network (CNN), have shown outstanding performance in analyzing tensor data, their wide adoption is still hindered by model complexity and lack of interpretability. To fill this research gap, we propose to use CP-decomposition to approximately compress the convolutional layer (CPAC-Conv layer) in deep learning. The contributions of our work could be summarized into three aspects: 1) we adapt CP-decomposition to compress convolutional kernels and derive the expressions of both forward and backward propagations for our proposed CPAC-Conv layer; 2) compared with the original convolutional layer, the proposed CPAC-Conv layer can reduce the number of parameters without decaying prediction performance. It can combine with other layers to build novel Neural Networks; 3) the value of decomposed kernels indicates the significance of the corresponding feature map, which increases model interpretability and provides us insights to guide feature selection.