Structured Estimation of Heterogeneous Time Series

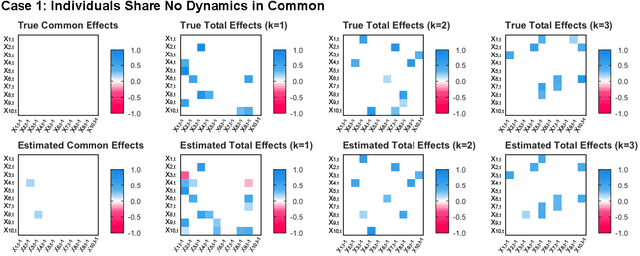
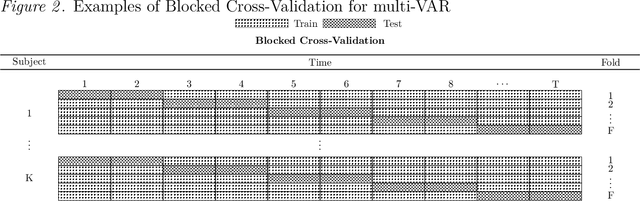
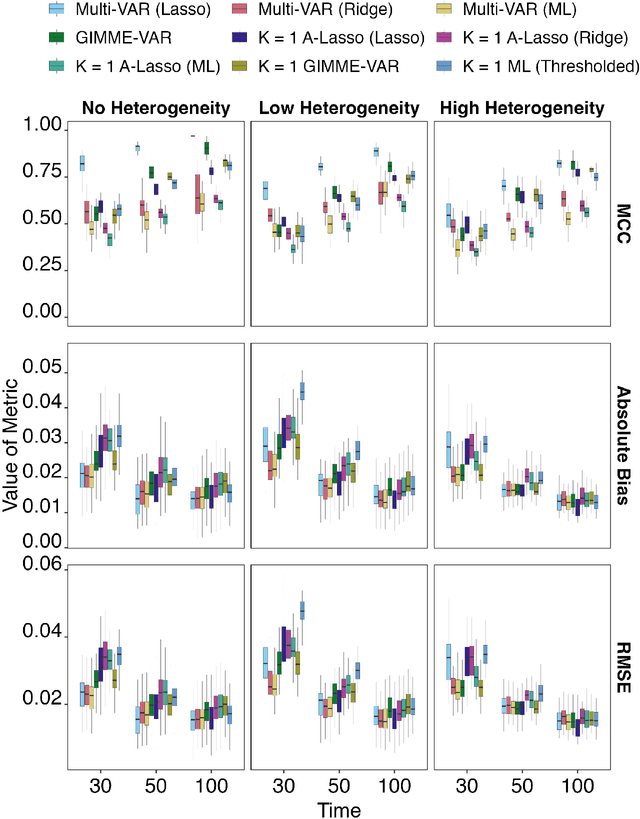
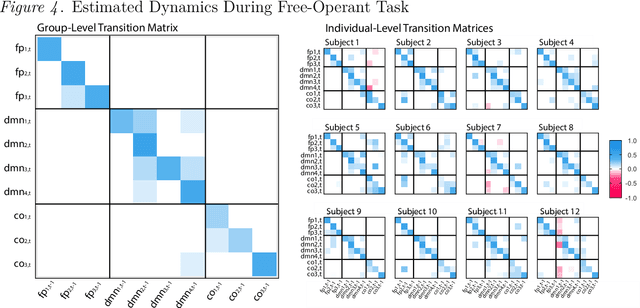
How best to model structurally heterogeneous processes is a foundational question in the social, health and behavioral sciences. Recently, Fisher et al., (2022) introduced the multi-VAR approach for simultaneously estimating multiple-subject multivariate time series characterized by common and individualizing features using penalized estimation. This approach differs from many popular modeling approaches for multiple-subject time series in that qualitative and quantitative differences in a large number of individual dynamics are well-accommodated. The current work extends the multi-VAR framework to include new adaptive weighting schemes that greatly improve estimation performance. In a small set of simulation studies we compare adaptive multi-VAR with these new penalty weights to common alternative estimators in terms of path recovery and bias. Furthermore, we provide toy examples and code demonstrating the utility of multi-VAR under different heterogeneity regimes using the multivar package for R (Fisher, 2022).

Consistency of Lloyd's Algorithm Under Perturbations

In the context of unsupervised learning, Lloyd's algorithm is one of the most widely used clustering algorithms. It has inspired a plethora of work investigating the correctness of the algorithm under various settings with ground truth clusters. In particular, in 2016, Lu and Zhou have shown that the mis-clustering rate of Lloyd's algorithm on $n$ independent samples from a sub-Gaussian mixture is exponentially bounded after $O(\log(n))$ iterations, assuming proper initialization of the algorithm. However, in many applications, the true samples are unobserved and need to be learned from the data via pre-processing pipelines such as spectral methods on appropriate data matrices. We show that the mis-clustering rate of Lloyd's algorithm on perturbed samples from a sub-Gaussian mixture is also exponentially bounded after $O(\log(n))$ iterations under the assumptions of proper initialization and that the perturbation is small relative to the sub-Gaussian noise. In canonical settings with ground truth clusters, we derive bounds for algorithms such as $k$-means$++$ to find good initializations and thus leading to the correctness of clustering via the main result. We show the implications of the results for pipelines measuring the statistical significance of derived clusters from data such as SigClust. We use these general results to derive implications in providing theoretical guarantees on the misclustering rate for Lloyd's algorithm in a host of applications, including high-dimensional time series, multi-dimensional scaling, and community detection for sparse networks via spectral clustering.

Block Dense Weighted Networks with Augmented Degree Correction

Dense networks with weighted connections often exhibit a community like structure, where although most nodes are connected to each other, different patterns of edge weights may emerge depending on each node's community membership. We propose a new framework for generating and estimating dense weighted networks with potentially different connectivity patterns across different communities. The proposed model relies on a particular class of functions which map individual node characteristics to the edges connecting those nodes, allowing for flexibility while requiring a small number of parameters relative to the number of edges. By leveraging the estimation techniques, we also develop a bootstrap methodology for generating new networks on the same set of vertices, which may be useful in circumstances where multiple data sets cannot be collected. Performance of these methods are analyzed in theory, simulations, and real data.

Penalized Estimation and Forecasting of Multiple Subject Intensive Longitudinal Data

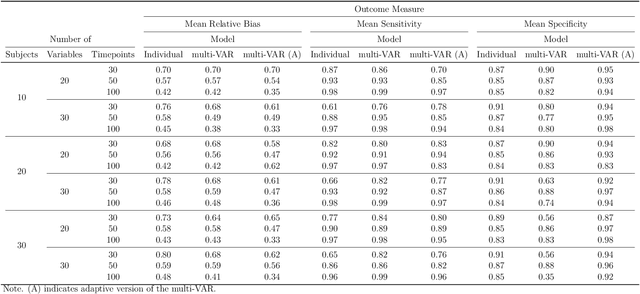
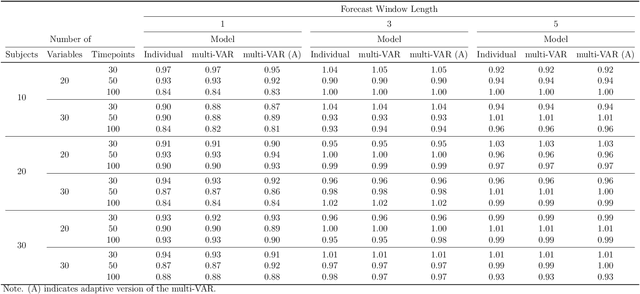
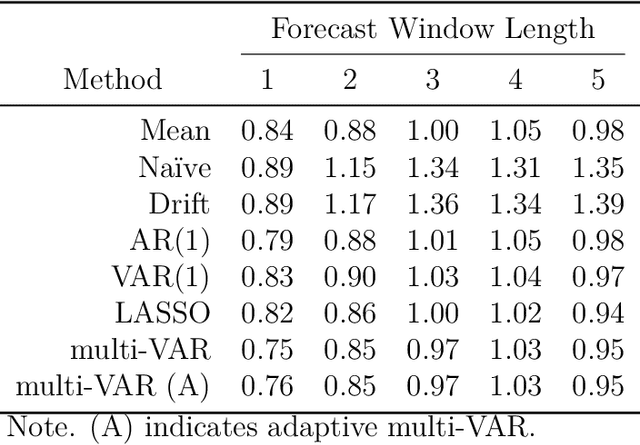
Intensive Longitudinal Data (ILD) is an increasingly common data type in the social and behavioral sciences. Despite the many benefits these data provide, little work has been dedicated to realizing the potential such data hold for forecasting dynamic processes at the individual level. To address this gap in the literature we present the multi-VAR framework, a novel methodological approach for penalized estimation and forecasting of ILD collected from multiple individuals. Importantly, our approach estimates models for all individuals simultaneously and is capable of adaptively adjusting to the amount of heterogeneity exhibited across individual dynamic processes. To accomplish this we propose proximal gradient descent algorithm for solving the multi-VAR problem and prove the consistency of the recovered transition matrices. We evaluate the forecasting performance of our method in comparison with a number of benchmark forecasting methods and provide an illustrative example involving the day-to-day emotional experiences of 16 individuals over an 11-week period.