Penalized Estimation and Forecasting of Multiple Subject Intensive Longitudinal Data
Paper and Code
Jul 09, 2020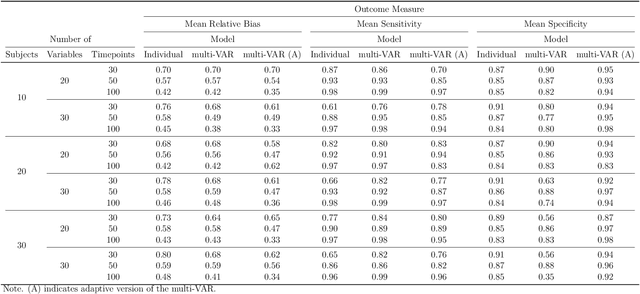

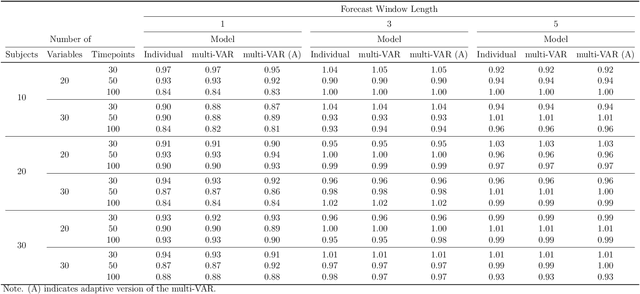
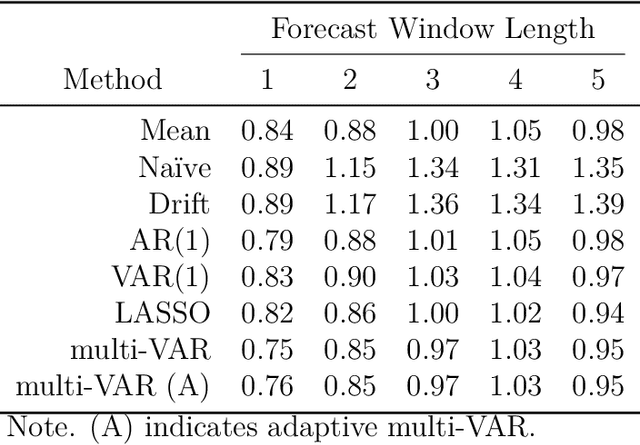
Intensive Longitudinal Data (ILD) is an increasingly common data type in the social and behavioral sciences. Despite the many benefits these data provide, little work has been dedicated to realizing the potential such data hold for forecasting dynamic processes at the individual level. To address this gap in the literature we present the multi-VAR framework, a novel methodological approach for penalized estimation and forecasting of ILD collected from multiple individuals. Importantly, our approach estimates models for all individuals simultaneously and is capable of adaptively adjusting to the amount of heterogeneity exhibited across individual dynamic processes. To accomplish this we propose proximal gradient descent algorithm for solving the multi-VAR problem and prove the consistency of the recovered transition matrices. We evaluate the forecasting performance of our method in comparison with a number of benchmark forecasting methods and provide an illustrative example involving the day-to-day emotional experiences of 16 individuals over an 11-week period.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge