Beyond Naïve Prompting: Strategies for Improved Zero-shot Context-aided Forecasting with LLMs

Forecasting in real-world settings requires models to integrate not only historical data but also relevant contextual information, often available in textual form. While recent work has shown that large language models (LLMs) can be effective context-aided forecasters via na\"ive direct prompting, their full potential remains underexplored. We address this gap with 4 strategies, providing new insights into the zero-shot capabilities of LLMs in this setting. ReDP improves interpretability by eliciting explicit reasoning traces, allowing us to assess the model's reasoning over the context independently from its forecast accuracy. CorDP leverages LLMs solely to refine existing forecasts with context, enhancing their applicability in real-world forecasting pipelines. IC-DP proposes embedding historical examples of context-aided forecasting tasks in the prompt, substantially improving accuracy even for the largest models. Finally, RouteDP optimizes resource efficiency by using LLMs to estimate task difficulty, and routing the most challenging tasks to larger models. Evaluated on different kinds of context-aided forecasting tasks from the CiK benchmark, our strategies demonstrate distinct benefits over na\"ive prompting across LLMs of different sizes and families. These results open the door to further simple yet effective improvements in LLM-based context-aided forecasting.

MVG-CRPS: A Robust Loss Function for Multivariate Probabilistic Forecasting

In probabilistic time series forecasting, the multivariate Gaussian (MVG) distribution is widely used as predictive distribution for correlated continuous random variables. Current deep probabilistic models typically employ neural networks to parameterize the mean vector and covariance matrix of the distribution, with log-score (i.e., negative log-likelihood) as the default loss function. However, log-score is highly sensitive to outliers, leading to significant errors when anomalies are present in the data. Motivated by the use of the continuous ranked probability score (CRPS) in learning univariate distributions, we propose a robust loss function specifically designed for high-dimensional MVG outputs. The proposed MVG-CRPS loss function has a closed-form expression based on the neural network outputs, making it easily integrable into deep learning models. We evaluate MVG-CRPS on two probabilistic forecasting tasks -- multivariate autoregressive and univariate sequence-to-sequence (Seq2Seq) forecasting -- both involving observations following MVG distribution. Experimental results on real-world datasets demonstrate that MVG-CRPS achieves both robustness and efficiency, offering enhanced accuracy and uncertainty quantification in probabilistic forecasting.

Multivariate Probabilistic Time Series Forecasting with Correlated Errors

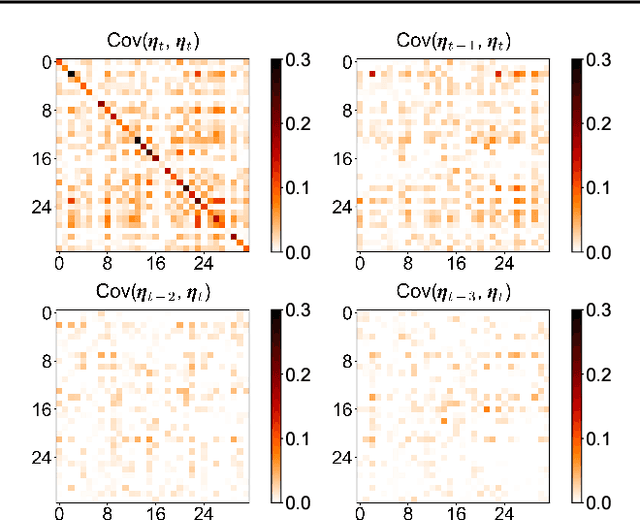
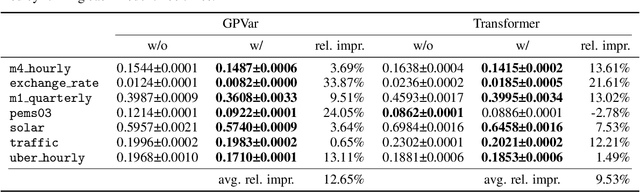
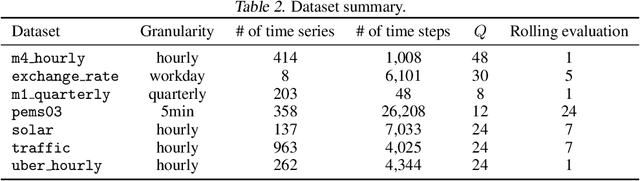
Modeling the correlations among errors is closely associated with how accurately the model can quantify predictive uncertainty in probabilistic time series forecasting. Recent multivariate models have made significant progress in accounting for contemporaneous correlations among errors, while a common assumption on these errors is that they are temporally independent for the sake of statistical simplicity. However, real-world observations often deviate from this assumption, since errors usually exhibit substantial autocorrelation due to various factors such as the exclusion of temporally correlated covariates. In this work, we propose an efficient method, based on a low-rank-plus-diagonal parameterization of the covariance matrix, which can effectively characterize the autocorrelation of errors. The proposed method possesses several desirable properties: the complexity does not scale with the number of time series, the resulting covariance can be used for calibrating predictions, and it can seamlessly integrate with any model with Gaussian-distributed errors. We empirically demonstrate these properties using two distinct neural forecasting models-GPVar and Transformer. Our experimental results confirm the effectiveness of our method in enhancing predictive accuracy and the quality of uncertainty quantification on multiple real-world datasets.

Better Batch for Deep Probabilistic Time Series Forecasting

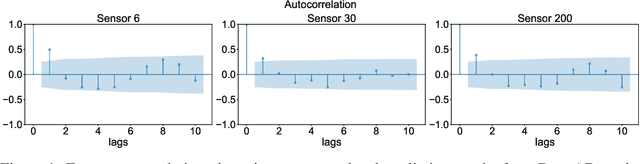
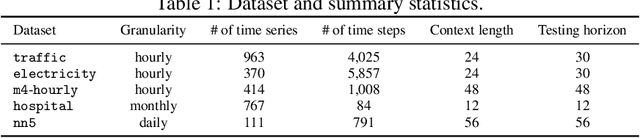
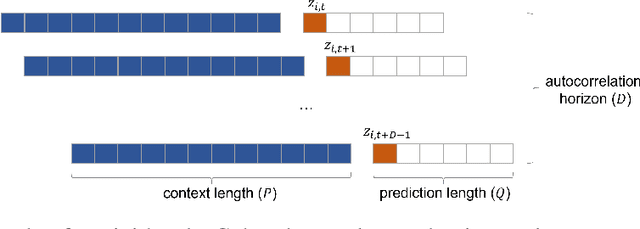
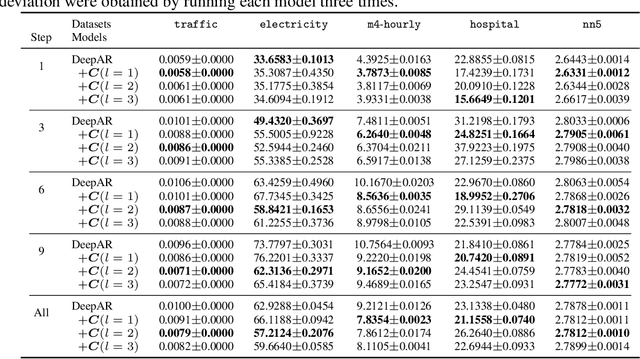
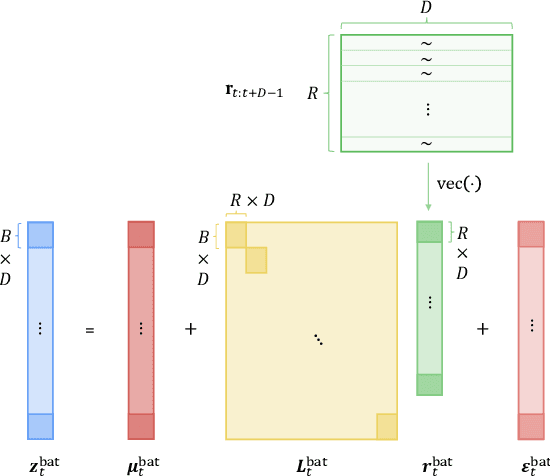
Deep probabilistic time series forecasting has gained significant attention due to its ability to provide valuable uncertainty quantification for decision-making tasks. However, many existing models oversimplify the problem by assuming the error process is time-independent, thereby overlooking the serial correlation in the error process. This oversight can potentially diminish the accuracy of the forecasts, rendering these models less effective for decision-making purposes. To overcome this limitation, we propose an innovative training method that incorporates error autocorrelation to enhance the accuracy of probabilistic forecasting. Our method involves constructing a mini-batch as a collection of $D$ consecutive time series segments for model training and explicitly learning a covariance matrix over each mini-batch that encodes the error correlation among adjacent time steps. The resulting covariance matrix can be used to improve prediction accuracy and enhance uncertainty quantification. We evaluate our method using DeepAR on multiple public datasets, and the experimental results confirm that our framework can effectively capture the error autocorrelation and enhance probabilistic forecasting.

Enhancing Deep Traffic Forecasting Models with Dynamic Regression

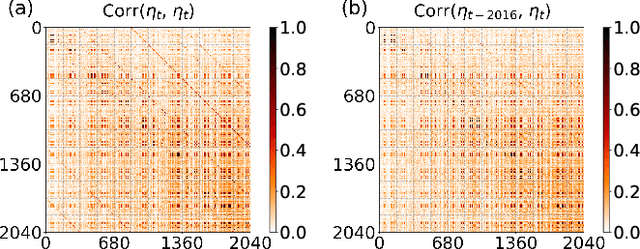
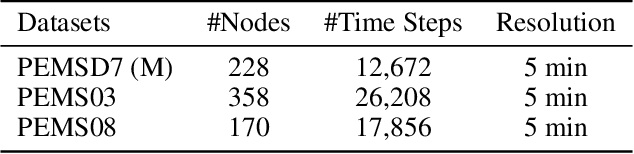
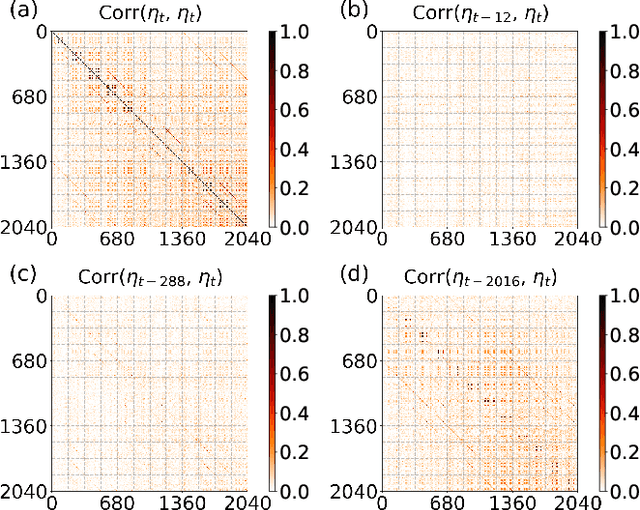
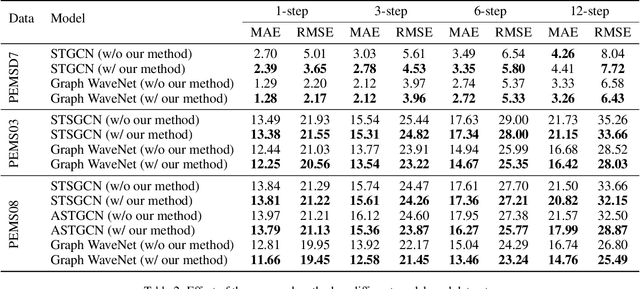
A common assumption in deep learning-based multivariate and multistep traffic time series forecasting models is that residuals are independent, isotropic, and uncorrelated in space and time. While this assumption provides a straightforward loss function (such as MAE/MSE), it is inevitable that residual processes will exhibit strong autocorrelation and structured spatiotemporal correlation. In this paper, we propose a complementary dynamic regression (DR) framework to enhance existing deep multistep traffic forecasting frameworks through structured specifications and learning for the residual process. Specifically, we assume the residuals of the base model (i.e., a well-developed traffic forecasting model) are governed by a matrix-variate seasonal autoregressive (AR) model, which can be seamlessly integrated into the training process by redesigning the overall loss function. Parameters in the DR framework can be jointly learned with the base model. We evaluate the effectiveness of the proposed framework in enhancing several state-of-the-art deep traffic forecasting models on both speed and flow datasets. Our experiment results show that the DR framework not only improves existing traffic forecasting models but also offers interpretable regression coefficients and spatiotemporal covariance matrices.