Multivariate Probabilistic Time Series Forecasting with Correlated Errors

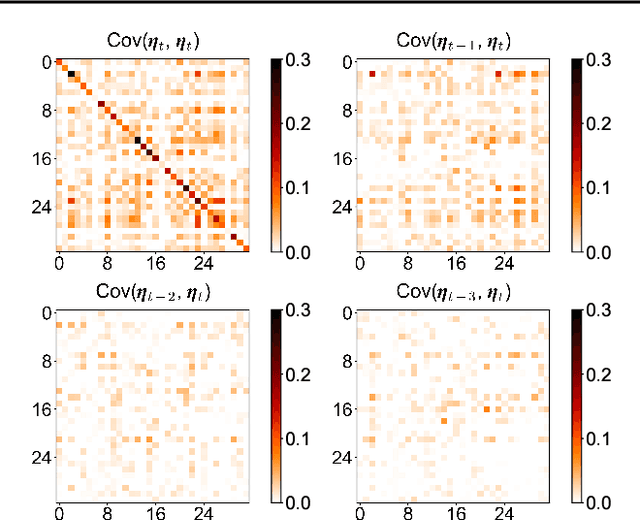
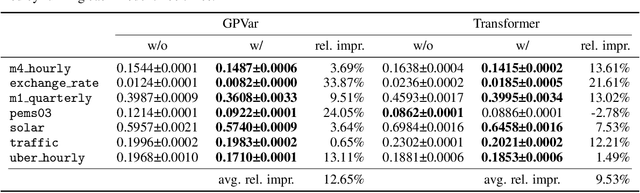
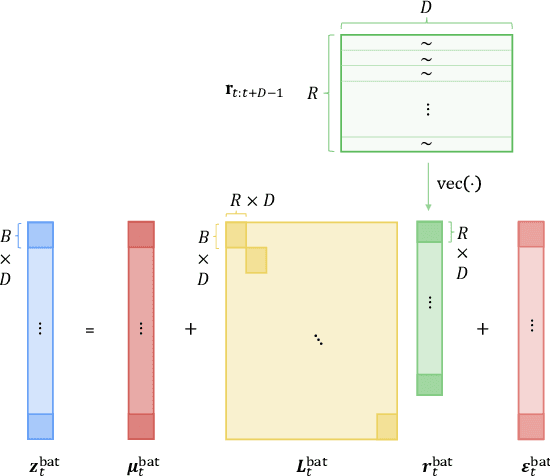
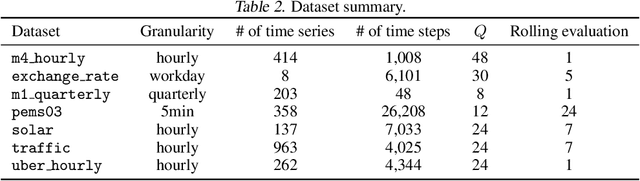
Modeling the correlations among errors is closely associated with how accurately the model can quantify predictive uncertainty in probabilistic time series forecasting. Recent multivariate models have made significant progress in accounting for contemporaneous correlations among errors, while a common assumption on these errors is that they are temporally independent for the sake of statistical simplicity. However, real-world observations often deviate from this assumption, since errors usually exhibit substantial autocorrelation due to various factors such as the exclusion of temporally correlated covariates. In this work, we propose an efficient method, based on a low-rank-plus-diagonal parameterization of the covariance matrix, which can effectively characterize the autocorrelation of errors. The proposed method possesses several desirable properties: the complexity does not scale with the number of time series, the resulting covariance can be used for calibrating predictions, and it can seamlessly integrate with any model with Gaussian-distributed errors. We empirically demonstrate these properties using two distinct neural forecasting models-GPVar and Transformer. Our experimental results confirm the effectiveness of our method in enhancing predictive accuracy and the quality of uncertainty quantification on multiple real-world datasets.