Enhancing Deep Traffic Forecasting Models with Dynamic Regression

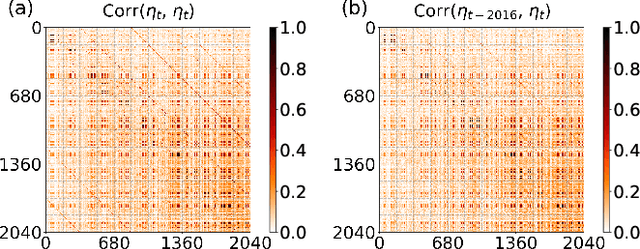
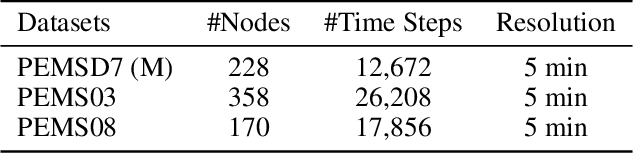
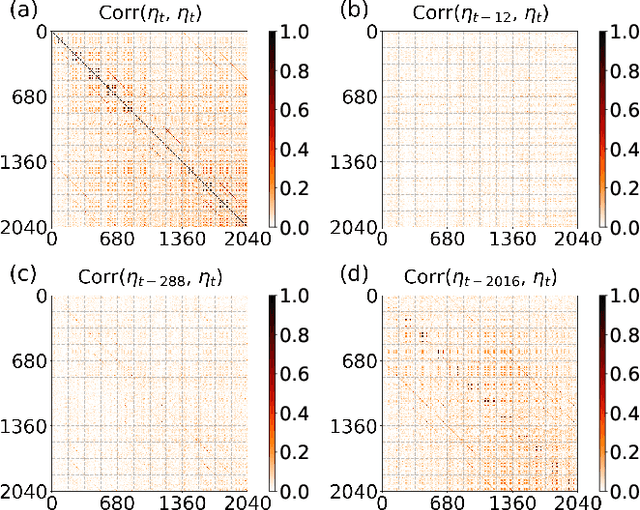
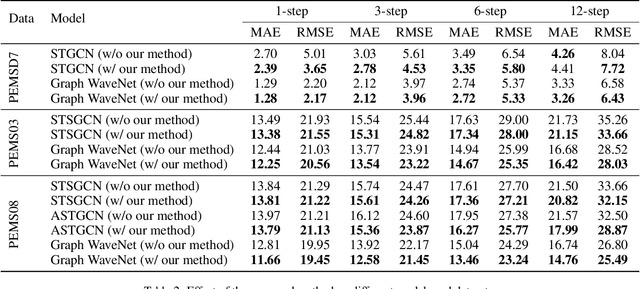
A common assumption in deep learning-based multivariate and multistep traffic time series forecasting models is that residuals are independent, isotropic, and uncorrelated in space and time. While this assumption provides a straightforward loss function (such as MAE/MSE), it is inevitable that residual processes will exhibit strong autocorrelation and structured spatiotemporal correlation. In this paper, we propose a complementary dynamic regression (DR) framework to enhance existing deep multistep traffic forecasting frameworks through structured specifications and learning for the residual process. Specifically, we assume the residuals of the base model (i.e., a well-developed traffic forecasting model) are governed by a matrix-variate seasonal autoregressive (AR) model, which can be seamlessly integrated into the training process by redesigning the overall loss function. Parameters in the DR framework can be jointly learned with the base model. We evaluate the effectiveness of the proposed framework in enhancing several state-of-the-art deep traffic forecasting models on both speed and flow datasets. Our experiment results show that the DR framework not only improves existing traffic forecasting models but also offers interpretable regression coefficients and spatiotemporal covariance matrices.