Parameterized Indexed Value Function for Efficient Exploration in Reinforcement Learning

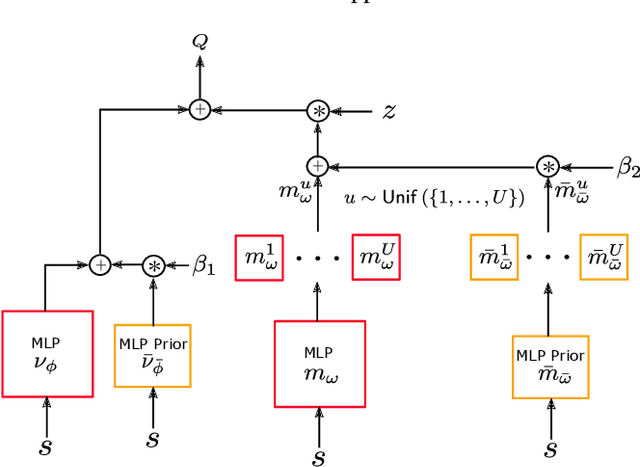
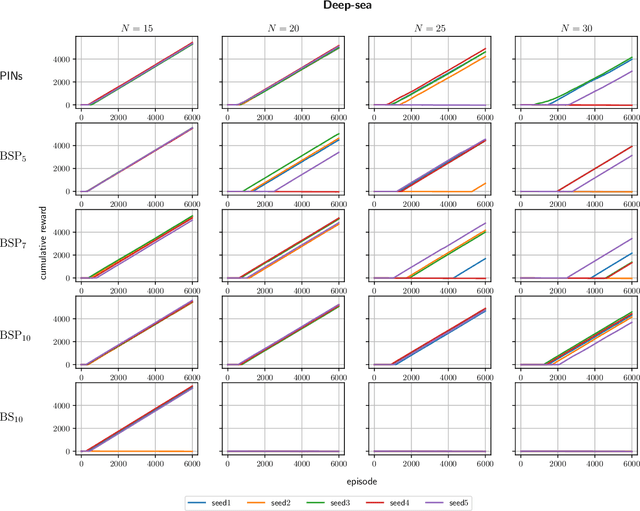
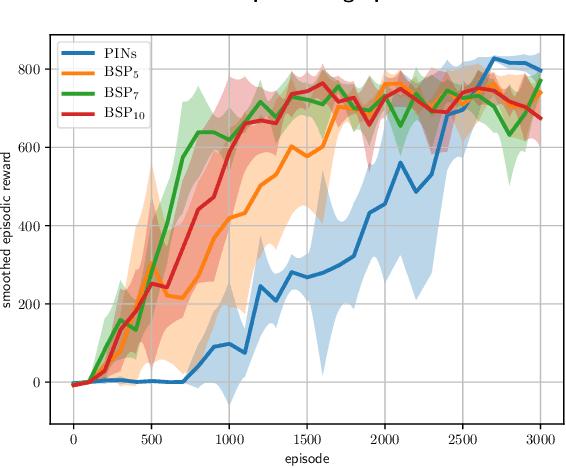
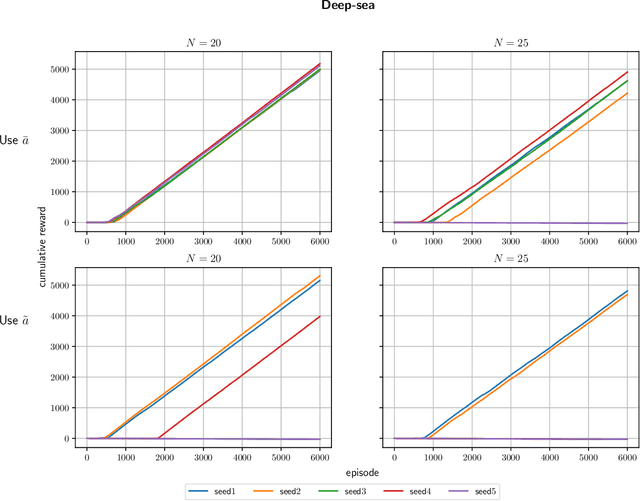
It is well known that quantifying uncertainty in the action-value estimates is crucial for efficient exploration in reinforcement learning. Ensemble sampling offers a relatively computationally tractable way of doing this using randomized value functions. However, it still requires a huge amount of computational resources for complex problems. In this paper, we present an alternative, computationally efficient way to induce exploration using index sampling. We use an indexed value function to represent uncertainty in our action-value estimates. We first present an algorithm to learn parameterized indexed value function through a distributional version of temporal difference in a tabular setting and prove its regret bound. Then, in a computational point of view, we propose a dual-network architecture, Parameterized Indexed Networks (PINs), comprising one mean network and one uncertainty network to learn the indexed value function. Finally, we show the efficacy of PINs through computational experiments.

Gradient Estimation with Simultaneous Perturbation and Compressive Sensing

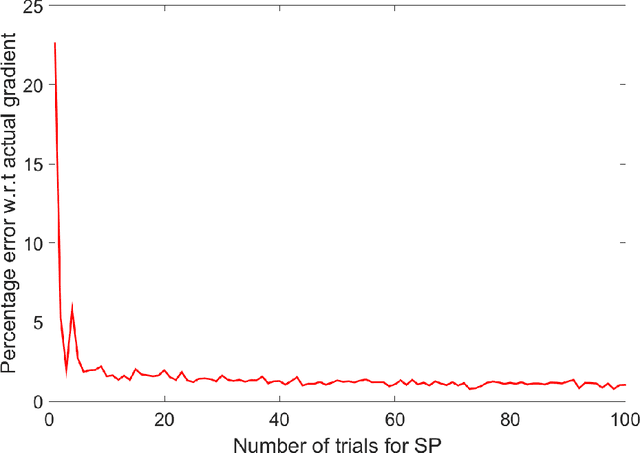
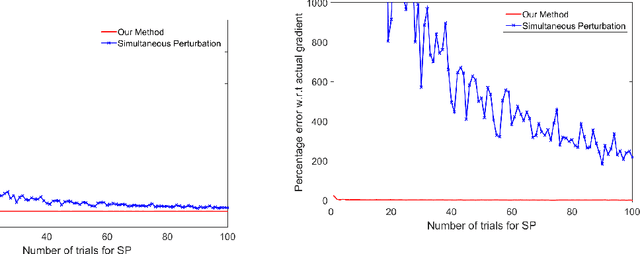
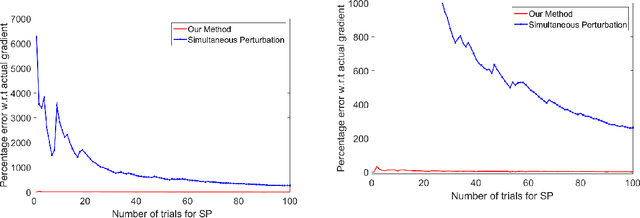
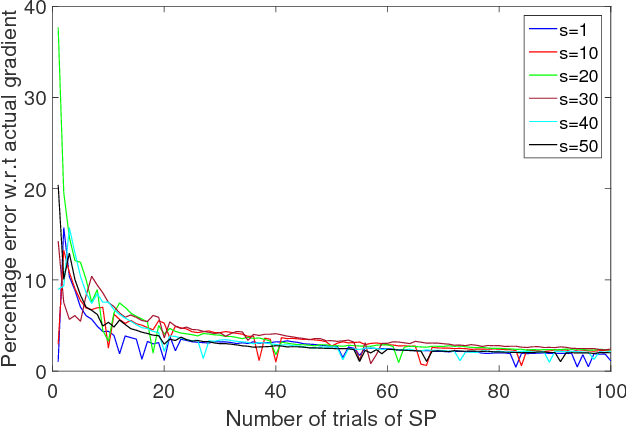
This paper aims at achieving a "good" estimator for the gradient of a function on a high-dimensional space. Often such functions are not sensitive in all coordinates and the gradient of the function is almost sparse. We propose a method for gradient estimation that combines ideas from Spall's Simultaneous Perturbation Stochastic Approximation with compressive sensing. The aim is to obtain "good" estimator without too many function evaluations. Application to estimating gradient outer product matrix as well as standard optimization problems are illustrated via simulations.