Parameterized Indexed Value Function for Efficient Exploration in Reinforcement Learning
Paper and Code
Dec 23, 2019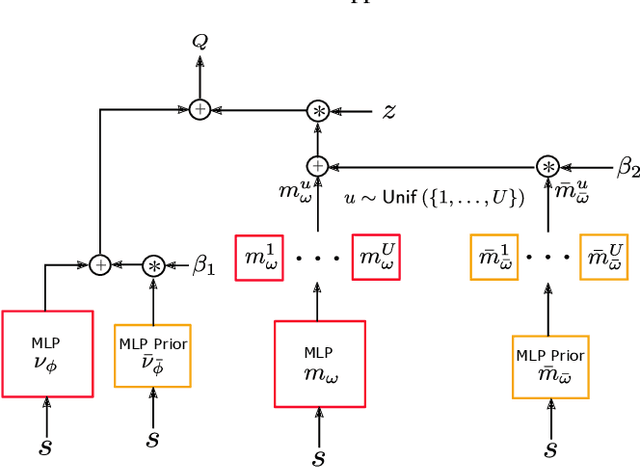
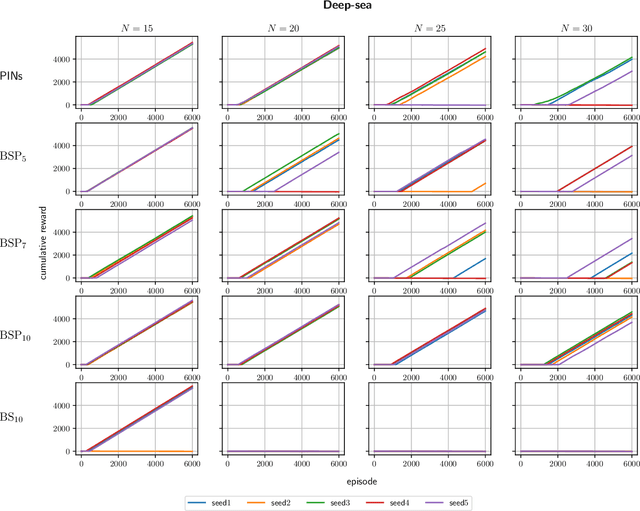
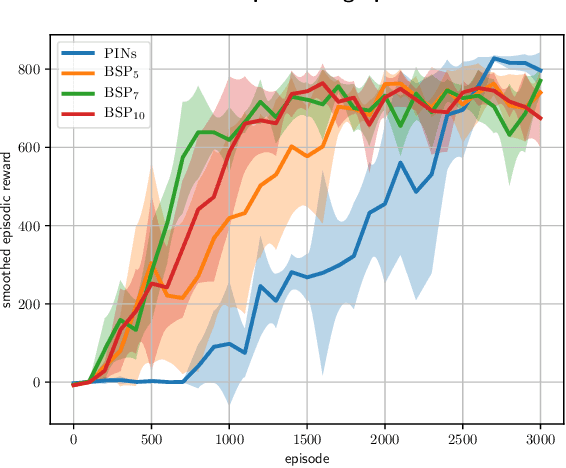
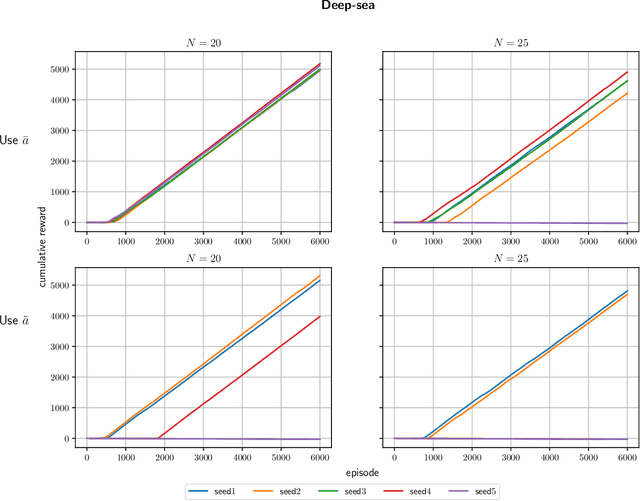
It is well known that quantifying uncertainty in the action-value estimates is crucial for efficient exploration in reinforcement learning. Ensemble sampling offers a relatively computationally tractable way of doing this using randomized value functions. However, it still requires a huge amount of computational resources for complex problems. In this paper, we present an alternative, computationally efficient way to induce exploration using index sampling. We use an indexed value function to represent uncertainty in our action-value estimates. We first present an algorithm to learn parameterized indexed value function through a distributional version of temporal difference in a tabular setting and prove its regret bound. Then, in a computational point of view, we propose a dual-network architecture, Parameterized Indexed Networks (PINs), comprising one mean network and one uncertainty network to learn the indexed value function. Finally, we show the efficacy of PINs through computational experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge