Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Neeraja Sahasrabudhe
Gradient Estimation with Simultaneous Perturbation and Compressive Sensing
Jul 26, 2016Figures and Tables: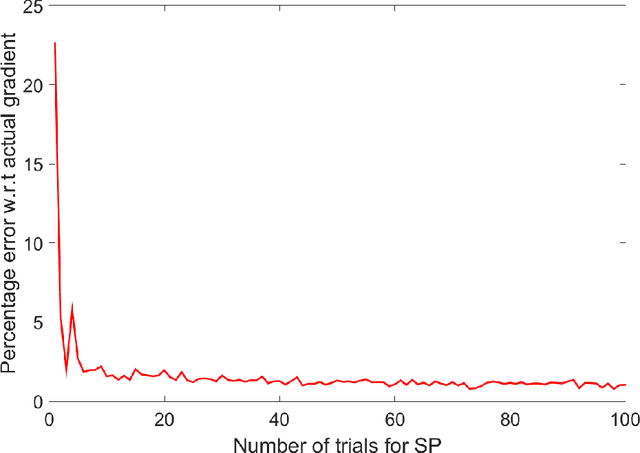
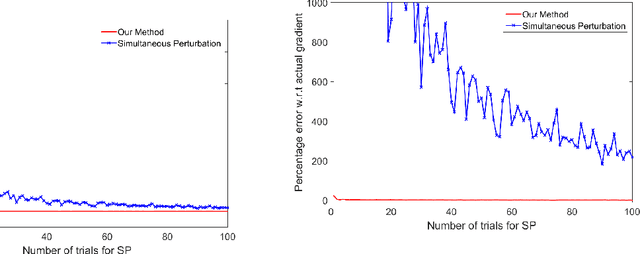
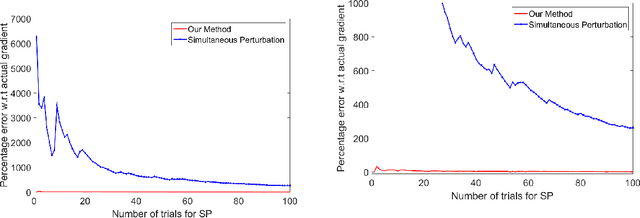
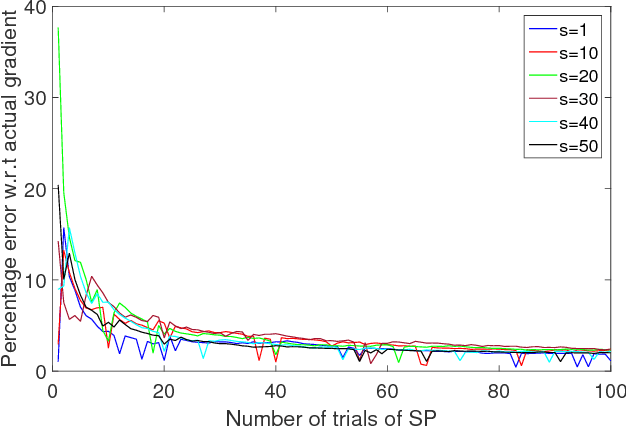




Abstract:This paper aims at achieving a "good" estimator for the gradient of a function on a high-dimensional space. Often such functions are not sensitive in all coordinates and the gradient of the function is almost sparse. We propose a method for gradient estimation that combines ideas from Spall's Simultaneous Perturbation Stochastic Approximation with compressive sensing. The aim is to obtain "good" estimator without too many function evaluations. Application to estimating gradient outer product matrix as well as standard optimization problems are illustrated via simulations.
* 24 pages, 13 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge