Supervised Linear Dimension-Reduction Methods: Review, Extensions, and Comparisons

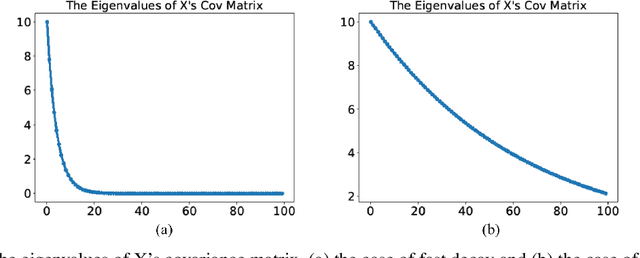
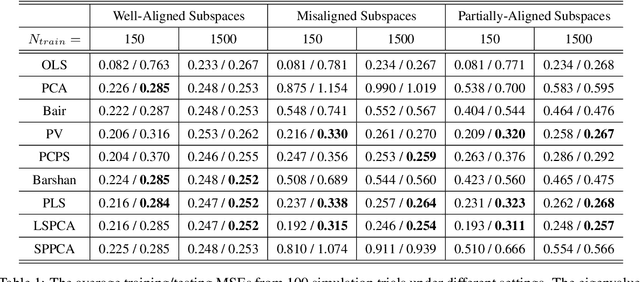
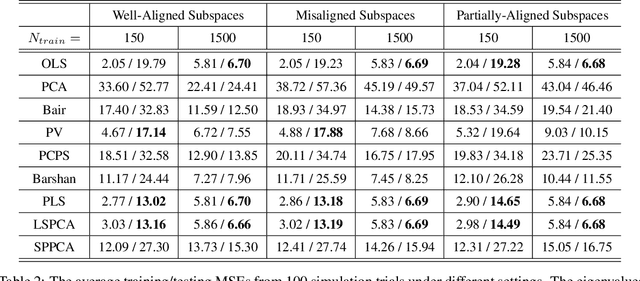
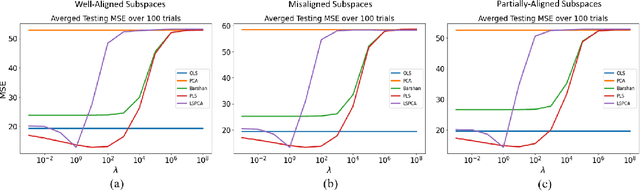
Principal component analysis (PCA) is a well-known linear dimension-reduction method that has been widely used in data analysis and modeling. It is an unsupervised learning technique that identifies a suitable linear subspace for the input variable that contains maximal variation and preserves as much information as possible. PCA has also been used in prediction models where the original, high-dimensional space of predictors is reduced to a smaller, more manageable, set before conducting regression analysis. However, this approach does not incorporate information in the response during the dimension-reduction stage and hence can have poor predictive performance. To address this concern, several supervised linear dimension-reduction techniques have been proposed in the literature. This paper reviews selected techniques, extends some of them, and compares their performance through simulations. Two of these techniques, partial least squares (PLS) and least-squares PCA (LSPCA), consistently outperform the others in this study.

Model Interpretation: A Unified Derivative-based Framework for Nonparametric Regression and Supervised Machine Learning

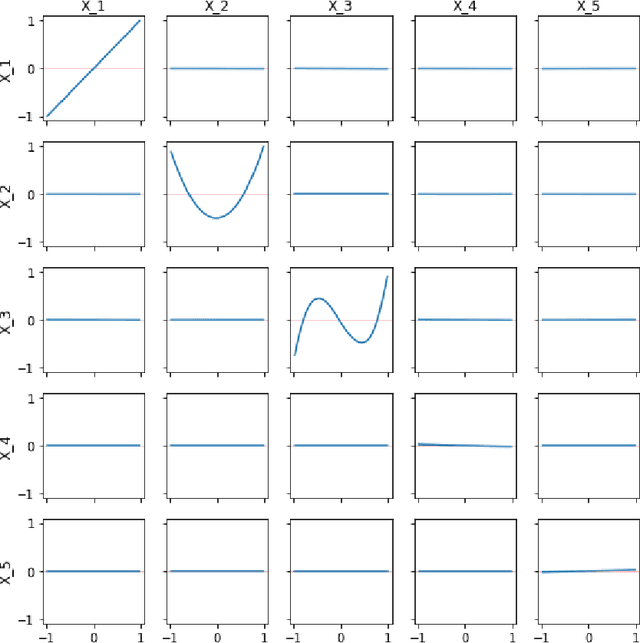
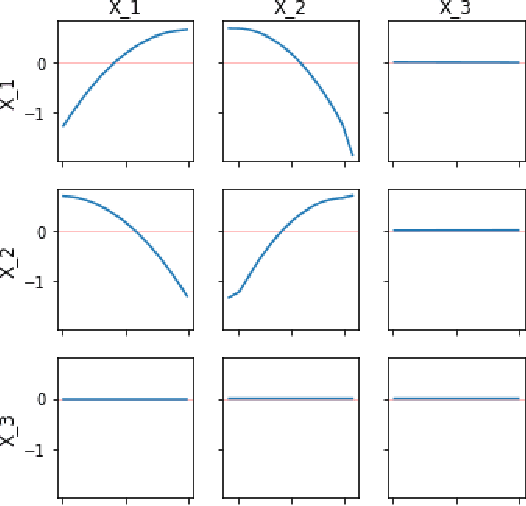
Interpreting a nonparametric regression model with many predictors is known to be a challenging problem. There has been renewed interest in this topic due to the extensive use of machine learning algorithms and the difficulty in understanding and explaining their input-output relationships. This paper develops a unified framework using a derivative-based approach for existing tools in the literature, including the partial-dependence plots, marginal plots and accumulated effects plots. It proposes a new interpretation technique called the accumulated total derivative effects plot and demonstrates how its components can be used to develop extensive insights in complex regression models with correlated predictors. The techniques are illustrated through simulation results.