Vernon M. Chinchilli
Probabilistic Model Incorporating Auxiliary Covariates to Control FDR
Oct 06, 2022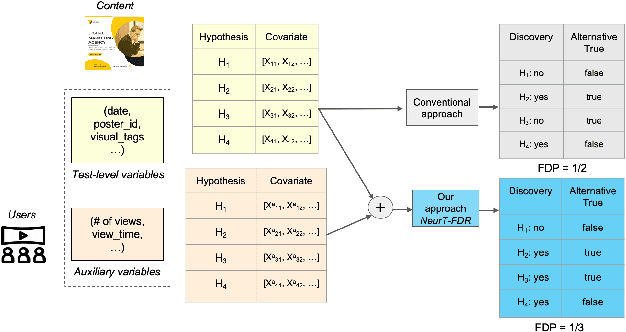
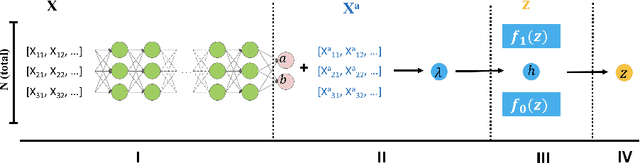
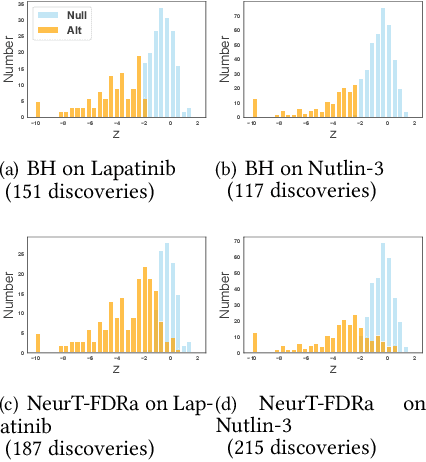
Abstract:Controlling False Discovery Rate (FDR) while leveraging the side information of multiple hypothesis testing is an emerging research topic in modern data science. Existing methods rely on the test-level covariates while ignoring metrics about test-level covariates. This strategy may not be optimal for complex large-scale problems, where indirect relations often exist among test-level covariates and auxiliary metrics or covariates. We incorporate auxiliary covariates among test-level covariates in a deep Black-Box framework controlling FDR (named as NeurT-FDR) which boosts statistical power and controls FDR for multiple-hypothesis testing. Our method parametrizes the test-level covariates as a neural network and adjusts the auxiliary covariates through a regression framework, which enables flexible handling of high-dimensional features as well as efficient end-to-end optimization. We show that NeurT-FDR makes substantially more discoveries in three real datasets compared to competitive baselines.
Variational Interpretable Learning from Multi-view Data
Mar 01, 2022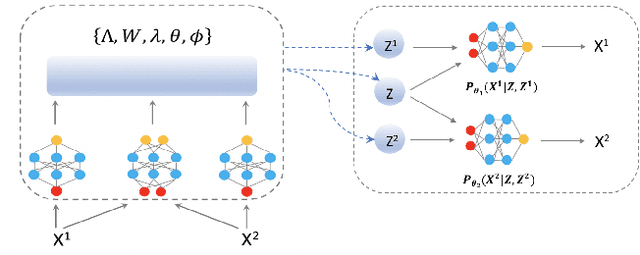



Abstract:The main idea of canonical correlation analysis (CCA) is to map different views onto a common latent space with maximum correlation. We propose a deep interpretable variational canonical correlation analysis (DICCA) for multi-view learning. The developed model extends the existing latent variable model for linear CCA to nonlinear models through the use of deep generative networks. DICCA is designed to disentangle both the shared and view-specific variations for multi-view data. To further make the model more interpretable, we place a sparsity-inducing prior on the latent weight with a structured variational autoencoder that is comprised of view-specific generators. Empirical results on real-world datasets show that our methods are competitive across domains.
NeurT-FDR: Controlling FDR by Incorporating Feature Hierarchy
Jan 24, 2021


Abstract:Controlling false discovery rate (FDR) while leveraging the side information of multiple hypothesis testing is an emerging research topic in modern data science. Existing methods rely on the test-level covariates while ignoring possible hierarchy among the covariates. This strategy may not be optimal for complex large-scale problems, where hierarchical information often exists among those test-level covariates. We propose NeurT-FDR which boosts statistical power and controls FDR for multiple hypothesis testing while leveraging the hierarchy among test-level covariates. Our method parametrizes the test-level covariates as a neural network and adjusts the feature hierarchy through a regression framework, which enables flexible handling of high-dimensional features as well as efficient end-to-end optimization. We show that NeurT-FDR has strong FDR guarantees and makes substantially more discoveries in synthetic and real datasets compared to competitive baselines.
Deep Latent Variable Model for Longitudinal Group Factor Analysis
May 11, 2020
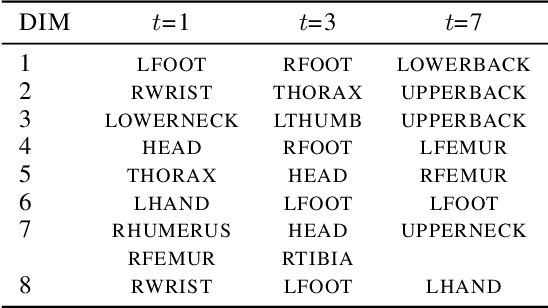
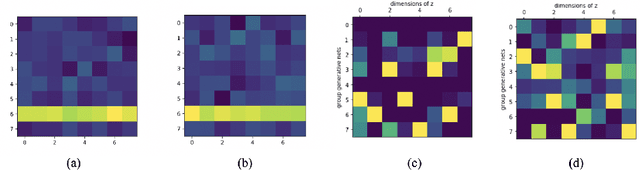

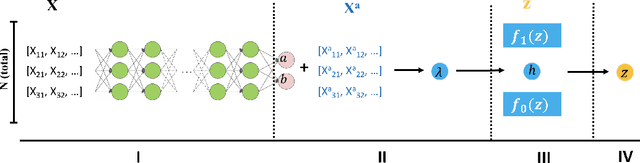
Abstract:In many scientific problems such as video surveillance, modern genomic analysis, and clinical studies, data are often collected from diverse domains across time that exhibit time-dependent heterogeneous properties. It is important to not only integrate data from multiple sources (called multiview data), but also to incorporate time dependency for deep understanding of the underlying system. Latent factor models are popular tools for exploring multi-view data. However, it is frequently observed that these models do not perform well for complex systems and they are not applicable to time-series data. Therefore, we propose a generative model based on variational autoencoder and recurrent neural network to infer the latent dynamic factors for multivariate timeseries data. This approach allows us to identify the disentangled latent embeddings across multiple modalities while accounting for the time factor. We invoke our proposed model for analyzing three datasets on which we demonstrate the effectiveness and the interpretability of the model.
Probabilistic Canonical Correlation Analysis for Sparse Count Data
May 11, 2020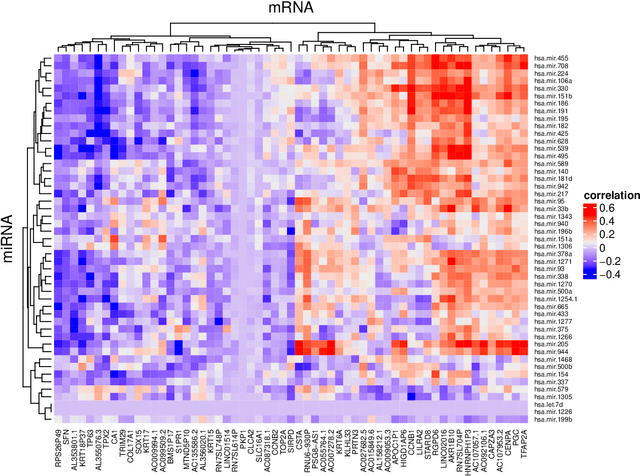

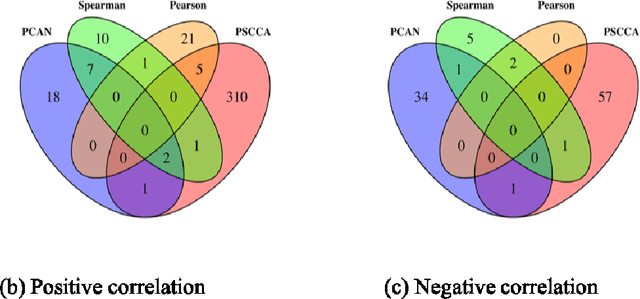

Abstract:Canonical correlation analysis (CCA) is a classical and important multivariate technique for exploring the relationship between two sets of continuous variables. CCA has applications in many fields, such as genomics and neuroimaging. It can extract meaningful features as well as use these features for subsequent analysis. Although some sparse CCA methods have been developed to deal with high-dimensional problems, they are designed specifically for continuous data and do not consider the integer-valued data from next-generation sequencing platforms that exhibit very low counts for some important features. We propose a model-based probabilistic approach for correlation and canonical correlation estimation for two sparse count data sets (PSCCA). PSCCA demonstrates that correlations and canonical correlations estimated at the natural parameter level are more appropriate than traditional estimation methods applied to the raw data. We demonstrate through simulation studies that PSCCA outperforms other standard correlation approaches and sparse CCA approaches in estimating the true correlations and canonical correlations at the natural parameter level. We further apply the PSCCA method to study the association of miRNA and mRNA expression data sets from a squamous cell lung cancer study, finding that PSCCA can uncover a large number of strongly correlated pairs than standard correlation and other sparse CCA approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge