Probabilistic Model Incorporating Auxiliary Covariates to Control FDR
Paper and Code
Oct 06, 2022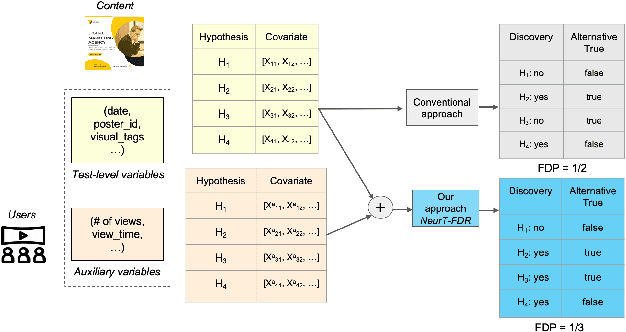
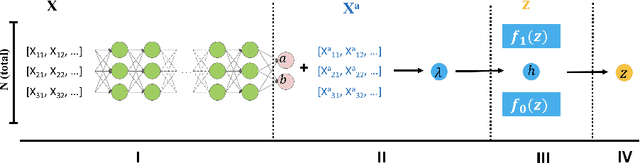
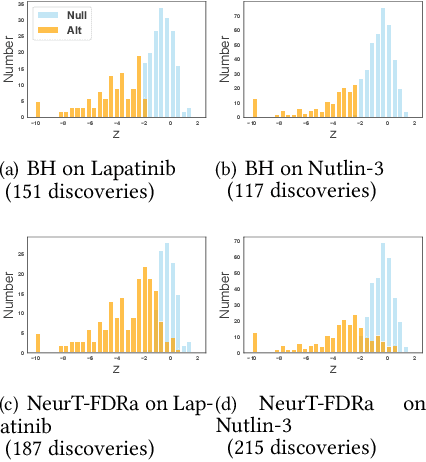
Controlling False Discovery Rate (FDR) while leveraging the side information of multiple hypothesis testing is an emerging research topic in modern data science. Existing methods rely on the test-level covariates while ignoring metrics about test-level covariates. This strategy may not be optimal for complex large-scale problems, where indirect relations often exist among test-level covariates and auxiliary metrics or covariates. We incorporate auxiliary covariates among test-level covariates in a deep Black-Box framework controlling FDR (named as NeurT-FDR) which boosts statistical power and controls FDR for multiple-hypothesis testing. Our method parametrizes the test-level covariates as a neural network and adjusts the auxiliary covariates through a regression framework, which enables flexible handling of high-dimensional features as well as efficient end-to-end optimization. We show that NeurT-FDR makes substantially more discoveries in three real datasets compared to competitive baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge