A Cantor-Kantorovich Metric Between Markov Decision Processes with Application to Transfer Learning

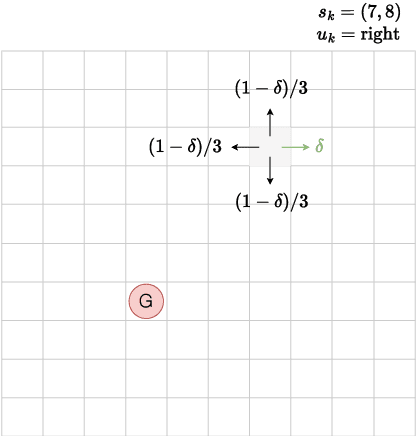
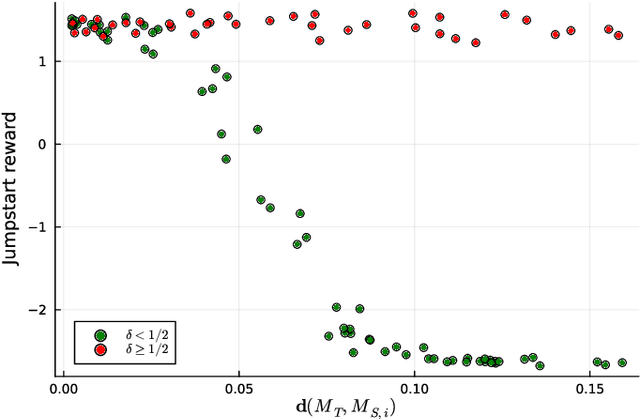
We extend the notion of Cantor-Kantorovich distance between Markov chains introduced by (Banse et al., 2023) in the context of Markov Decision Processes (MDPs). The proposed metric is well-defined and can be efficiently approximated given a finite horizon. Then, we provide numerical evidences that the latter metric can lead to interesting applications in the field of reinforcement learning. In particular, we show that it could be used for forecasting the performance of transfer learning algorithms.

Path Planning Using Wassertein Distributionally Robust Deep Q-learning

We investigate the problem of risk averse robot path planning using the deep reinforcement learning and distributionally robust optimization perspectives. Our problem formulation involves modelling the robot as a stochastic linear dynamical system, assuming that a collection of process noise samples is available. We cast the risk averse motion planning problem as a Markov decision process and propose a continuous reward function design that explicitly takes into account the risk of collision with obstacles while encouraging the robot's motion towards the goal. We learn the risk-averse robot control actions through Lipschitz approximated Wasserstein distributionally robust deep Q-learning to hedge against the noise uncertainty. The learned control actions result in a safe and risk averse trajectory from the source to the goal, avoiding all the obstacles. Various supporting numerical simulations are presented to demonstrate our proposed approach.

Distributionally Robust RRT with Risk Allocation

An integration of distributionally robust risk allocation into sampling-based motion planning algorithms for robots operating in uncertain environments is proposed. We perform non-uniform risk allocation by decomposing the distributionally robust joint risk constraints defined over the entire planning horizon into individual risk constraints given the total risk budget. Specifically, the deterministic tightening defined using the individual risk constraints is leveraged to define our proposed exact risk allocation procedure. Our idea of embedding the risk allocation technique into sampling based motion planning algorithms realises guaranteed conservative, yet increasingly more risk feasible trajectories for efficient state space exploration.

Risk-Averse RRT* Planning with Nonlinear Steering and Tracking Controllers for Nonlinear Robotic Systems Under Uncertainty

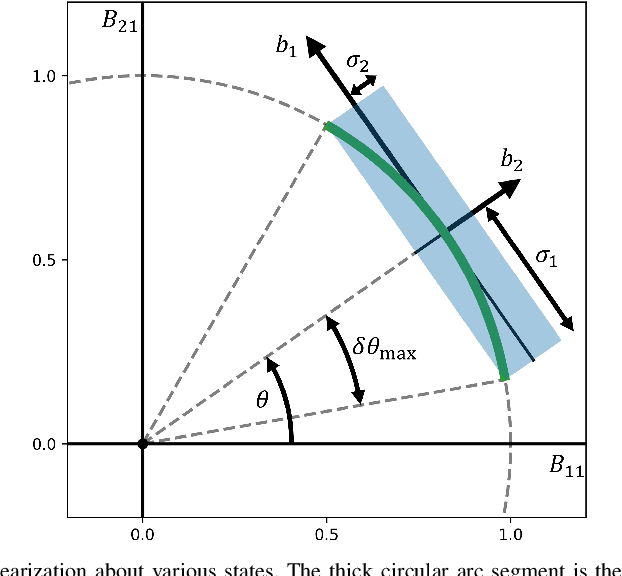
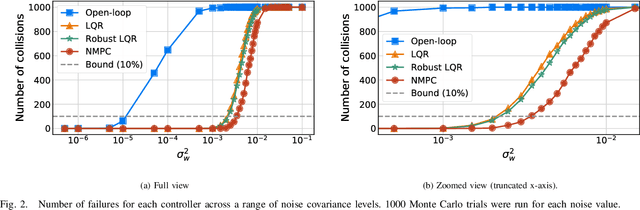
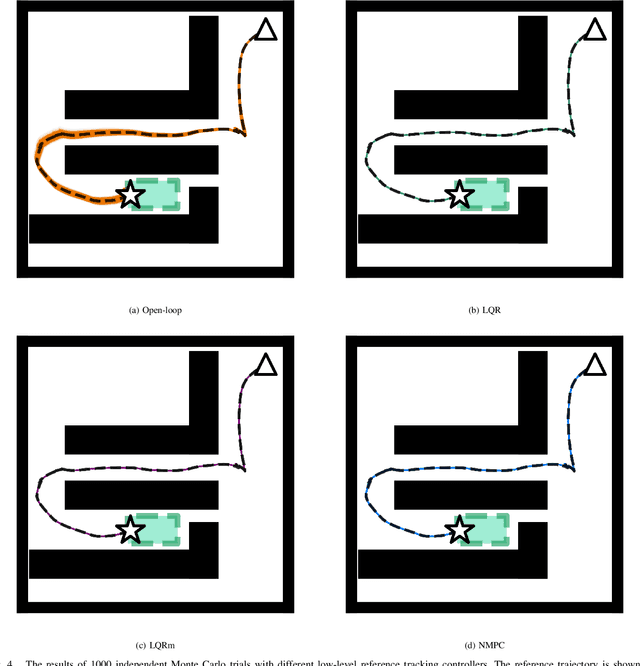
We propose a two-phase risk-averse architecture for controlling stochastic nonlinear robotic systems. We present Risk-Averse Nonlinear Steering RRT* (RANS-RRT*) as an RRT* variant that incorporates nonlinear dynamics by solving a nonlinear program (NLP) and accounts for risk by approximating the state distribution and performing a distributionally robust (DR) collision check to promote safe planning.The generated plan is used as a reference for a low-level tracking controller. We demonstrate three controllers: finite horizon linear quadratic regulator (LQR) with linearized dynamics around the reference trajectory, LQR with robustness-promoting multiplicative noise terms, and a nonlinear model predictive control law (NMPC). We demonstrate the effectiveness of our algorithm using unicycle dynamics under heavy-tailed Laplace process noise in a cluttered environment.